Notes
angles of a polygon

Angles of a Polygon

There are two angles formed at each vertex of a polygon: the interior and exterior angles.

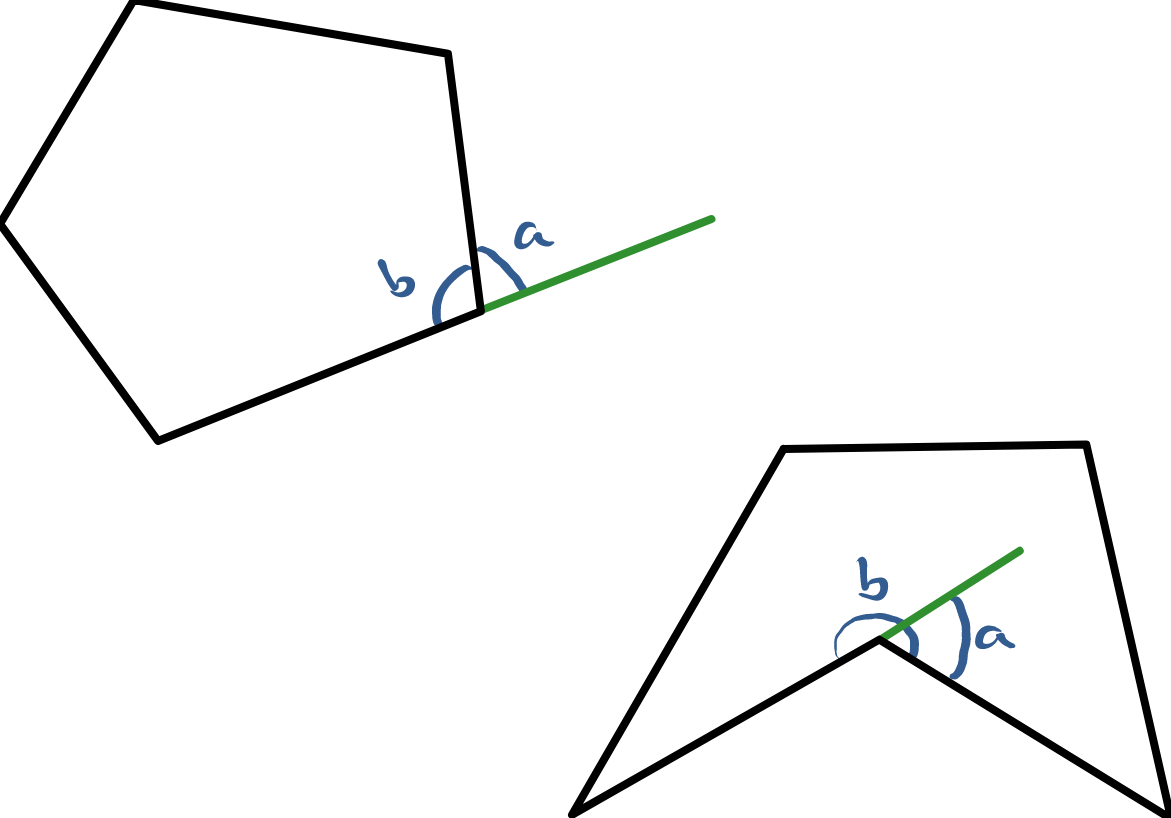
The interior angle at a vertex is the angle that is formed by the two edges that meet at that vertex and which lies inside the polygon. The exterior angle is formed by extending an edge through the vertex and taking the angle between this extension and the other edge.

Strictly speaking, exterior angles are signed and should be considered together with a clockwise or anti-clockwise direction. With this convention, the interior and exterior angles at a vertex always add up to $180^\circ$.

Sums of angles

Taken with signs, the exterior angles of a polygon add up to $360^\circ$. This can be viewed as saying that as one walks around a polygon, one turns through a single full turn. If the polygon has concave vertices, the exterior angles have to be taken with their signs to indicate their direction.

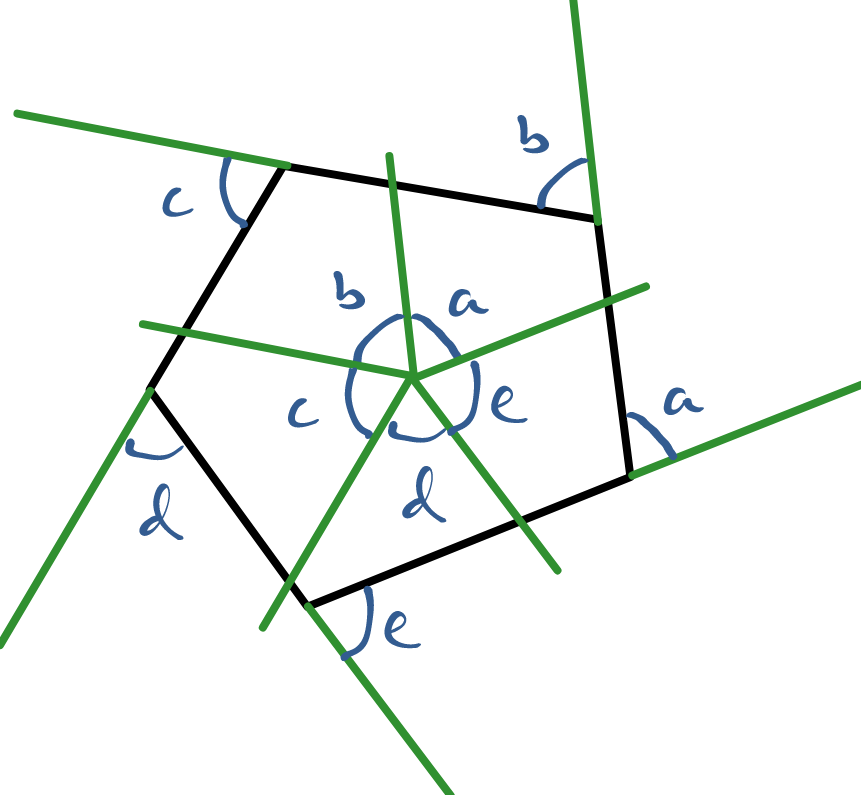
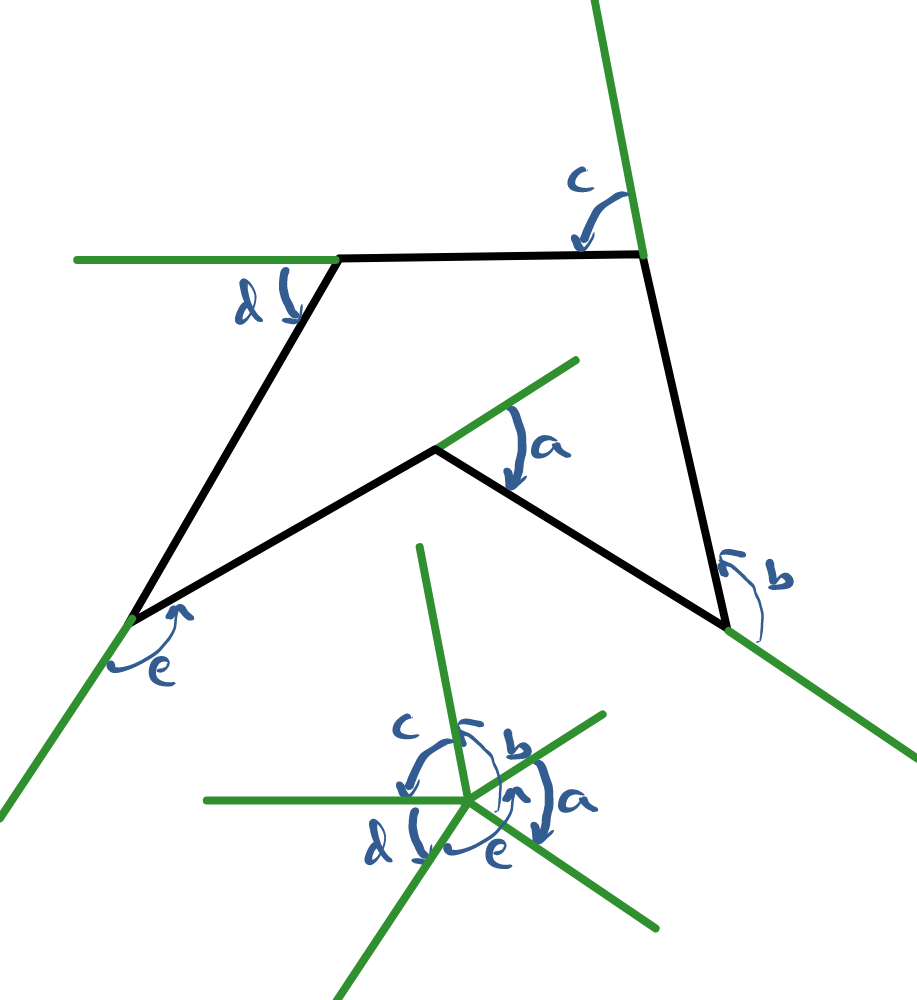
The interior angles of an $n$-sided polygon add up to $180^\circ(n-2)$. This follows from the fact that the exterior angles add up to $360^\circ$ and at each vertex then the interior and exterior angles add up to $180^\circ$. So adding up all the interior and exterior angles is $180^\circ$ times the number of sides, then taking away the $360^\circ$ for the sum of the exteriors gives $180^\circ(n-2)$ for the sum of the interiors.