Notes
tilted triangles solution
Solution to the Tilted Triangles Puzzle
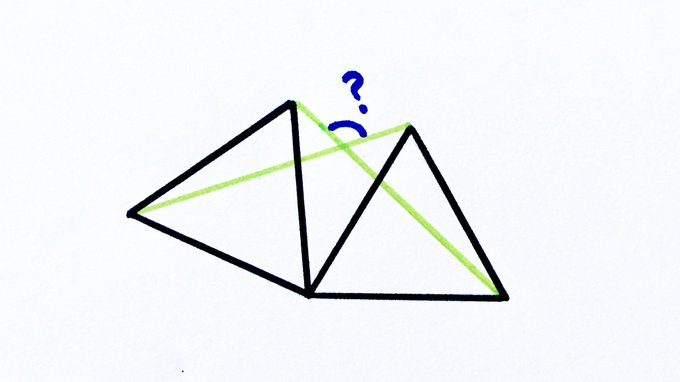
The two equilateral triangles are congruent. What’s the angle?
Solution by Angle at the Centre is Twice the Angle at the Circumference
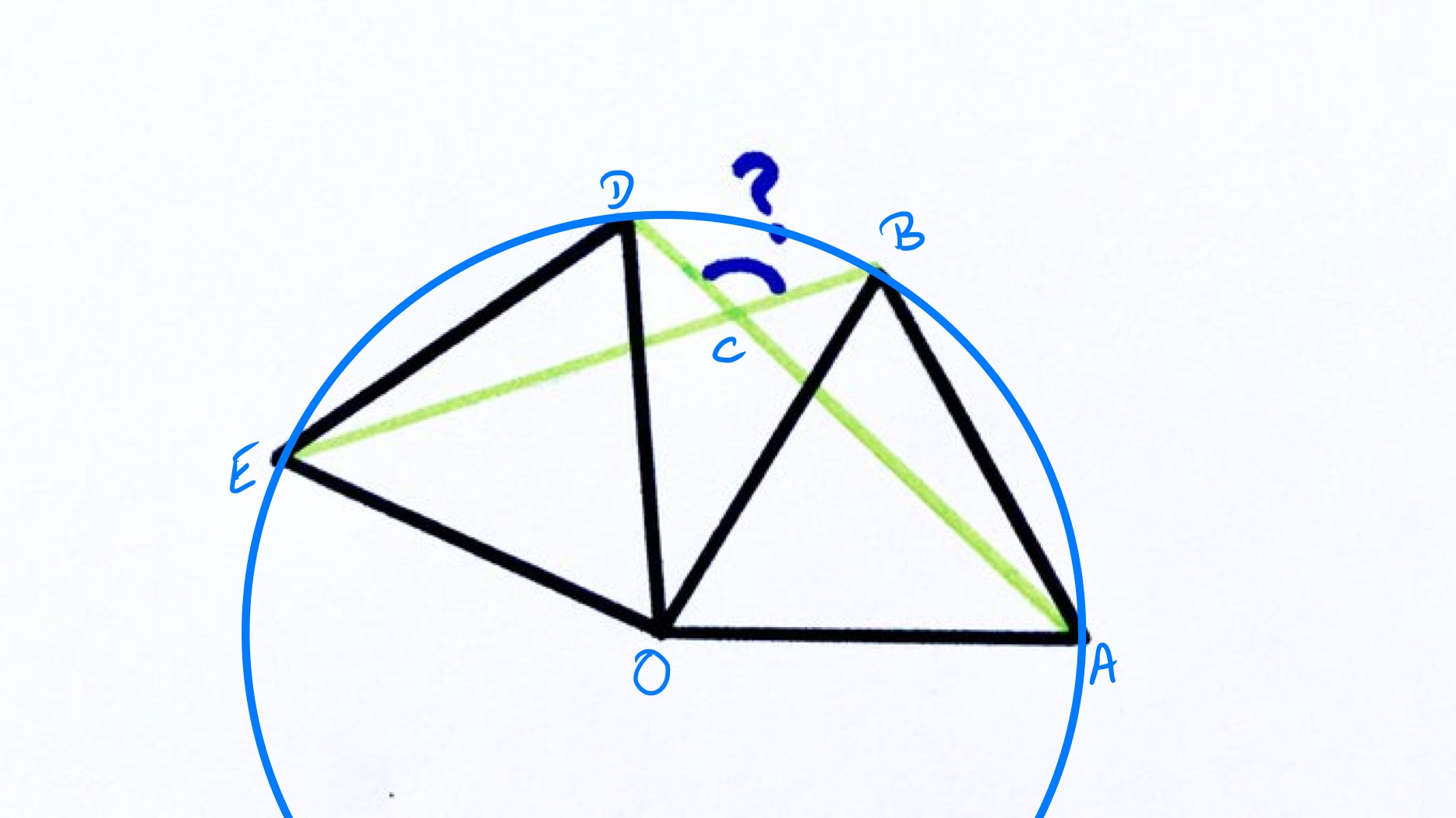
With the points labelled as in the above diagram, since the triangles are equilateral and congruent the lengths of , , , and are all the same so the circle centred on that passes through also passes through , , and .
Since the angle at the centre is twice the angle at the circumference, the reflex angle is twice angle . The same argument shows that angle is twice angle . Adding together angles and therefore gives half of the sum of and . Angles and are both the interior angle of an equilateral triangle so are . Since the angles at a point add up to , this means that angles and add up to . Then as the angles in a triangle add up to , angle is and so is .