Notes
two hexagons and a triangle solution
Solution to the Puzzle
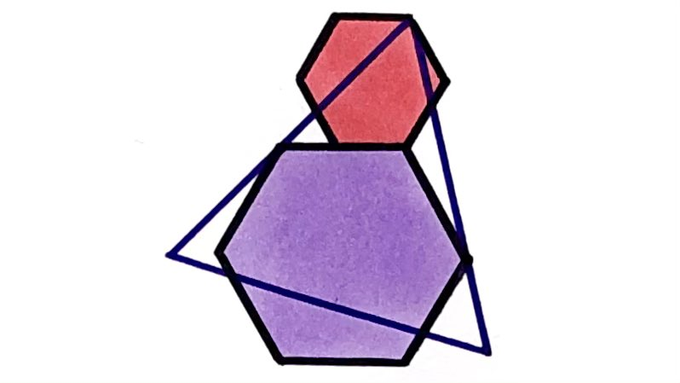
All three polygons here are regular. The area of the small hexagon is . What’s the area of the large one?
Solution by Angle at the Centre is Twice the Angle at the Circumference
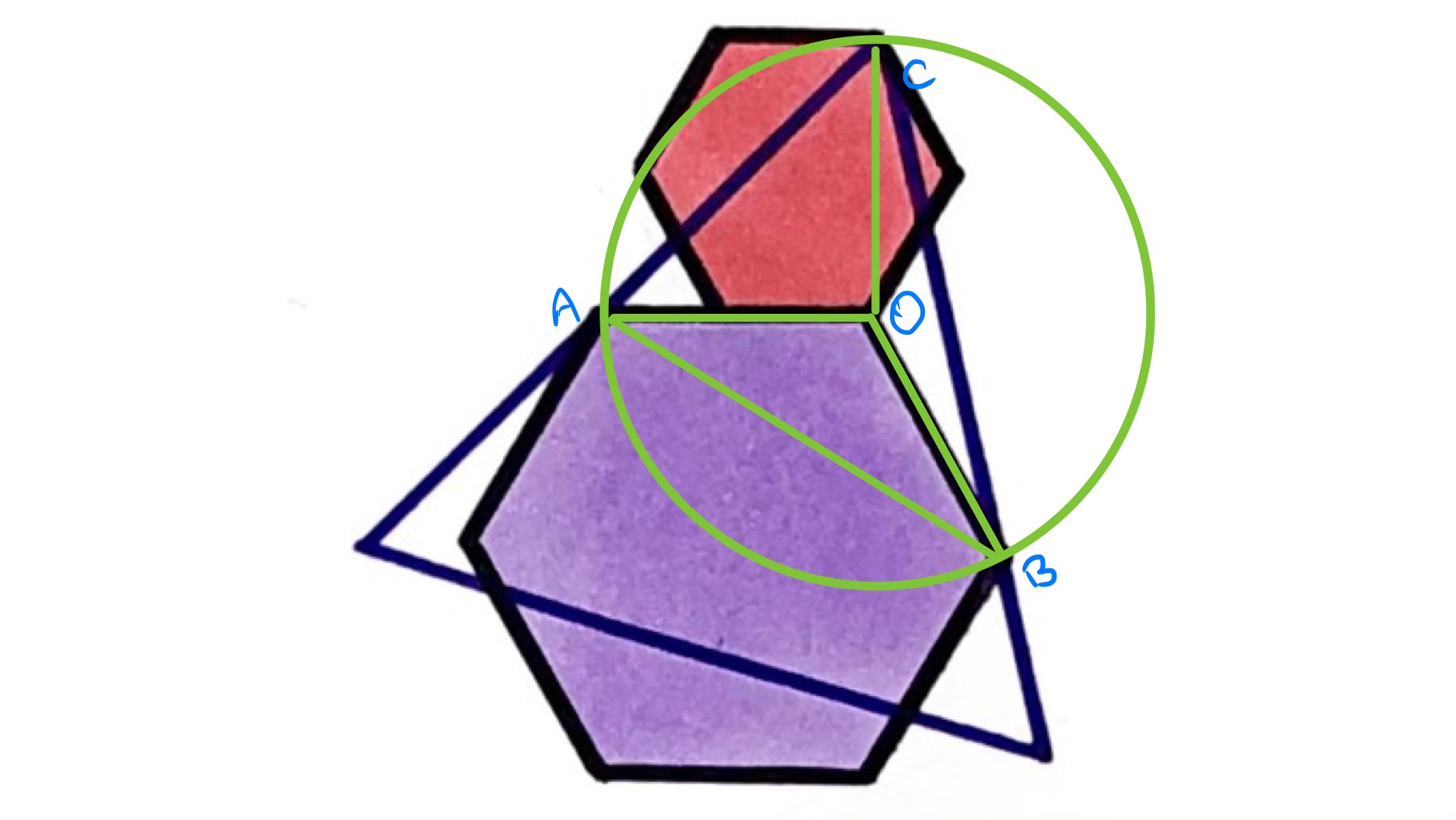
With the points labelled as above, consider the circle centre through . As the purple hexagon is regular, so this circle also passes through . The angle is as it is the interior angle in a regular hexagon. Angle is as the interior angle in an equilateral triangle which is half . Hence by the fact that the angle at the centre is twice the angle at the circumference, lies on the circle. Hence .
Now is times the side length of the smaller hexagon (see the page on hexagons for how the various lengths are related) so the scale factor from the red hexagon to the purple hexagon is and hence the area scale factor is .
Thus the area of the larger hexagon is .