Notes
two circles in a square ii solution

Solution to the Two Circles in a Square II Puzzle

Solution by Angles in a Polygon, Angle Between a Radius and Tangent, and Isosceles Triangle

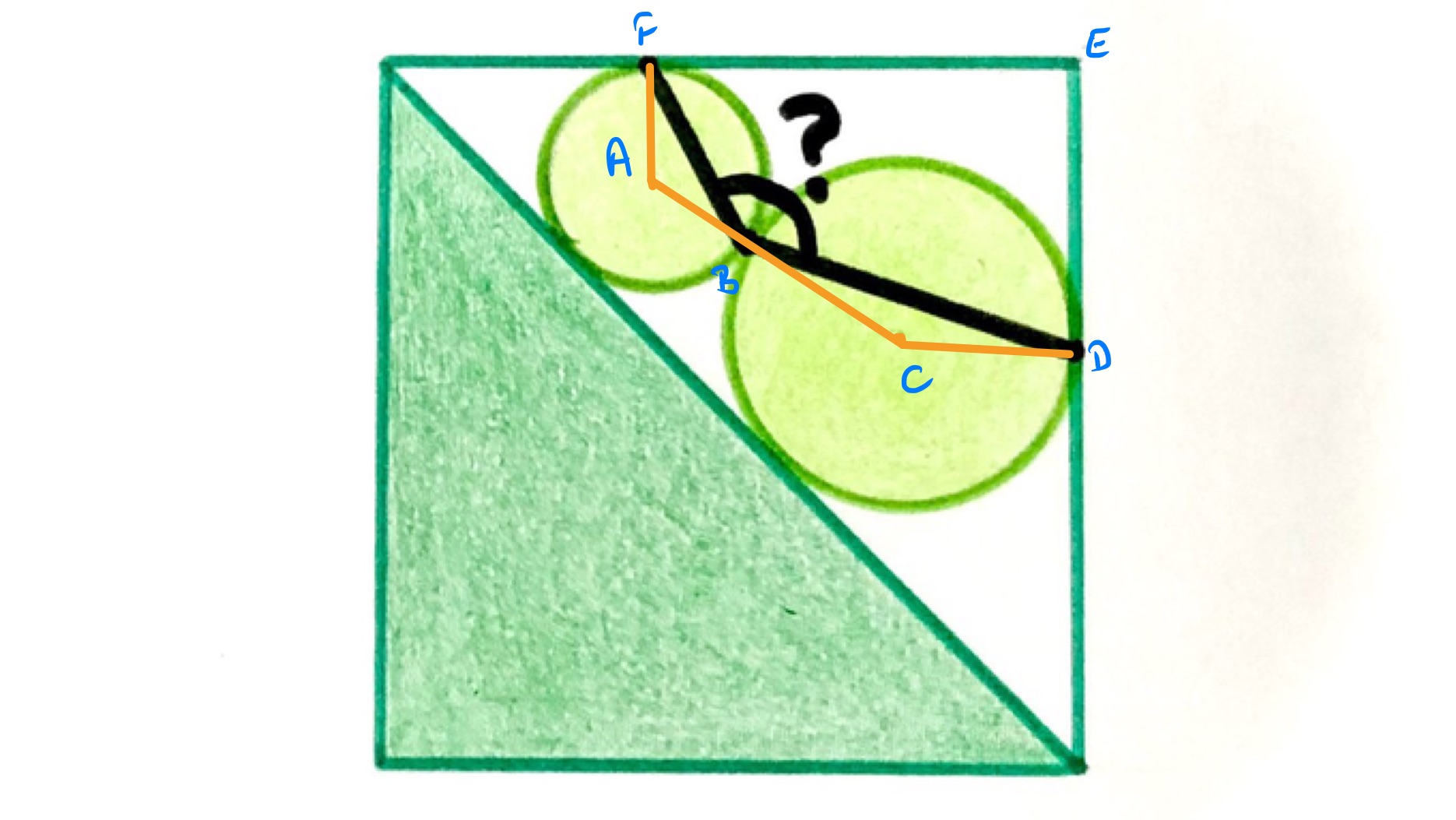
In the above diagram, $A$ and $C$ are the centres of the circles.

The shape $A C D E F$ is a pentagon and so the sum of its interior angles is $540^\circ$. Three of its angles are right-angles: $F \hat{E} D$ is the interior angle of a square while $A\hat{F}E$ and $E \hat{D} C$ are the angle between a radius and tangent. The remaining angles must therefore add up to $540^\circ - 3 \times 90^\circ = 270^\circ$.

Triangles $C D B$ and $A B F$ are both isosceles as $A$ and $C$ are the centres of their respective circles. Angle $C \hat{B} D$ is half of what remains after angle $D \hat{C} B$ is taken away from $180^\circ$ and similar for angle $F \hat{B} A$. So the sum of these two angles is given by:

The requested angle is $180^\circ - (F \hat{B}A + D \hat{C} B)$ and so is $\frac{1}{2} ( B \hat{A} F + D \hat{C} B) = \frac{270^\circ}{2} = 135^\circ$.

(Note that the fact that the circles touch the diagonal line is not needed. This result holds for any two circles that are tangent to each other and to a pair of perpendicular lines.)