Notes
pentagon with two semi-circles solution
Solution to the Pentagon with two Semi-Circles Puzzle
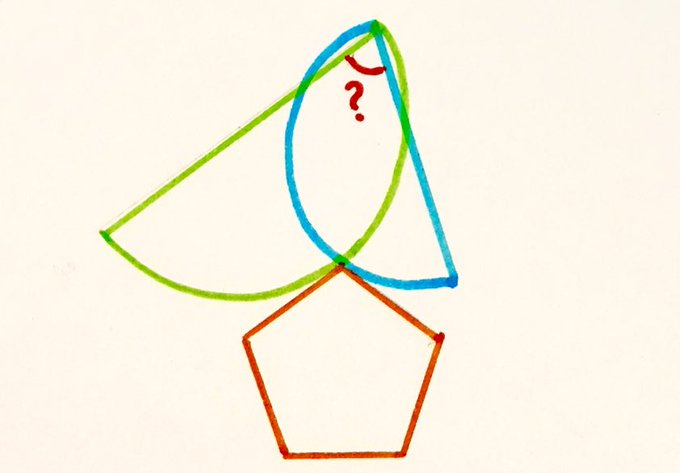
The regular pentagon is tangent to both semicircles at the point where the three meet. What’s the angle between the bases of the semicircles? What if I started with other regular polygons?
Solution by Angle Between a Radius and Tangent and Angles in a Regular Pentagon
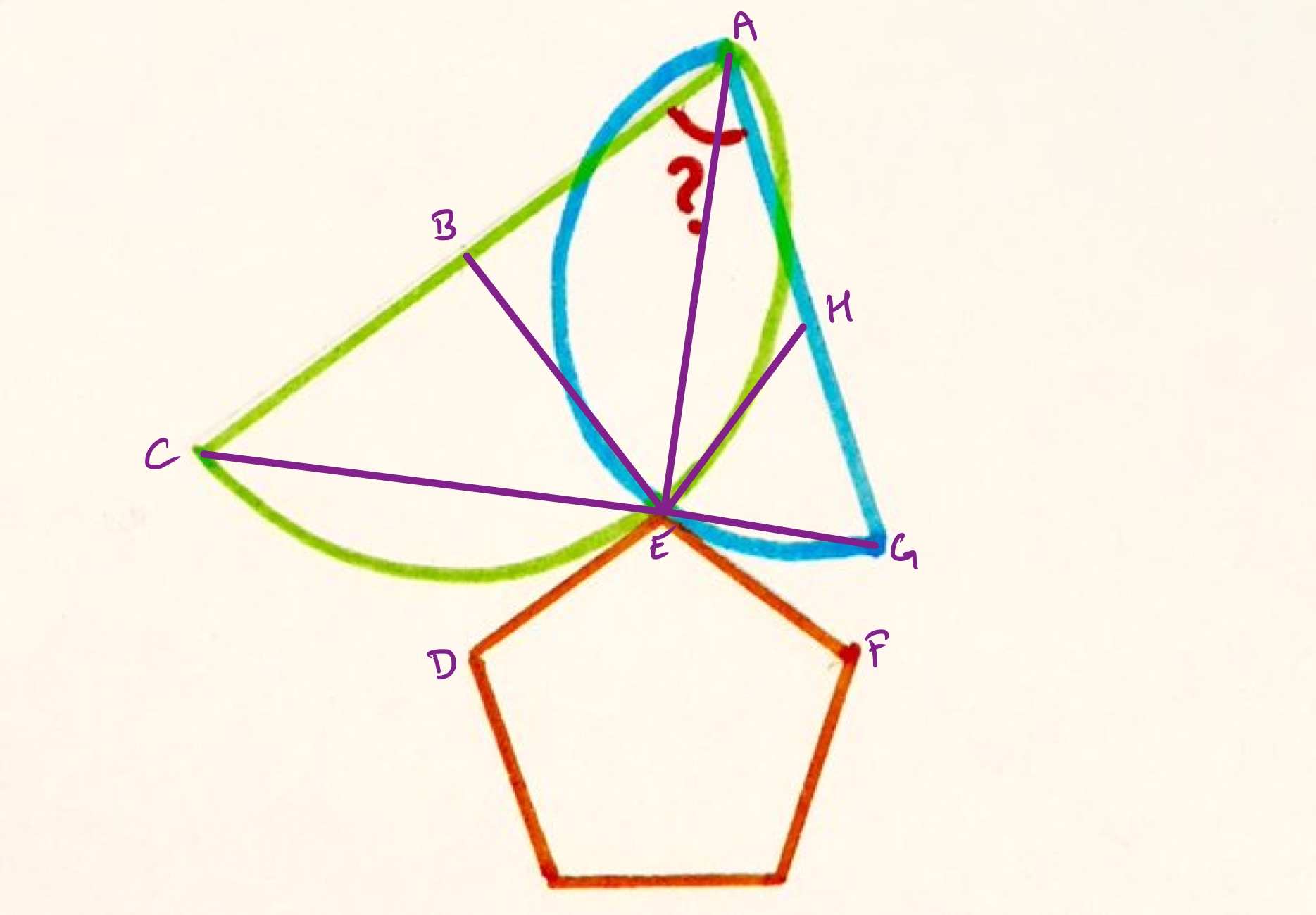
In the above diagram, the points labelled and are the centres of their semi-circles.
Since the angle between a radius and tangent is , angles and are both . Angle is the interior angle in a regular pentagon so is . Since the angles at a point add up to , this leaves for angle .
Triangles and are both isosceles, so angles are are equal and therefore the angle between the bases of the semi-circles is .