Notes
two regular hexagons iii solution
Solution to the Two Regular Hexagons (III) Puzzle
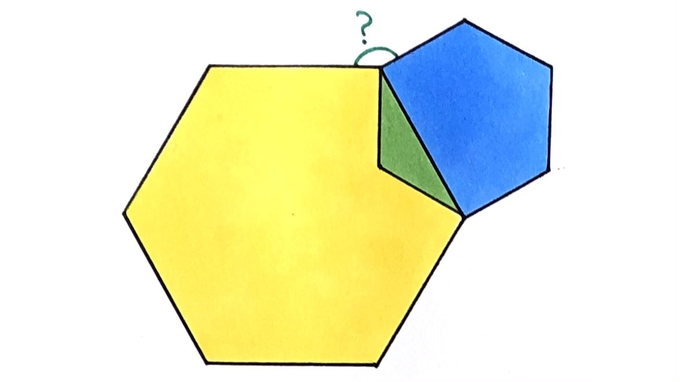
Both hexagons are regular. What’s the angle?
Solution by Calculating Angles
To calculate the indicated angle, consider the rest of the turn. This consists of two interior angles of hexagons with an overlap. The interior angle of a hexagon is .
There are a couple of ways to calculate the overlap. The green area is an isosceles triangle, with apex angle the interior angle of the smaller hexagon, so the base angle (which is the overlap angle) is half of , which is . Alternatively, the base of that line joins two parallel sides of the hexagon and so by symmetry is perpendicular to those sides. The overlap angle is therefore .
The angle to be calculated is therefore: