Notes
a hexagon and a nonagon solution
Solution to the Puzzle
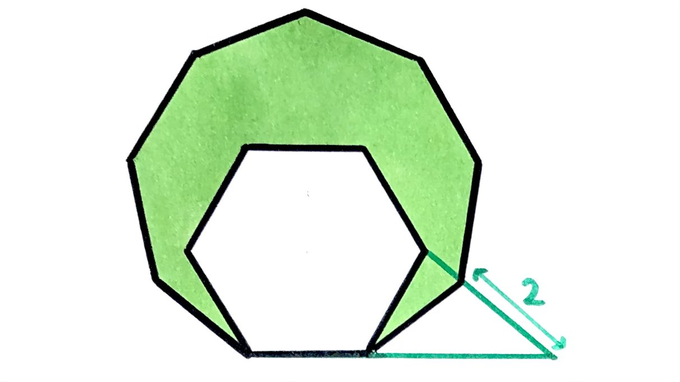
Two regular polygons. What’s the perimeter of the shaded region?
Solution by Angles in a triangle
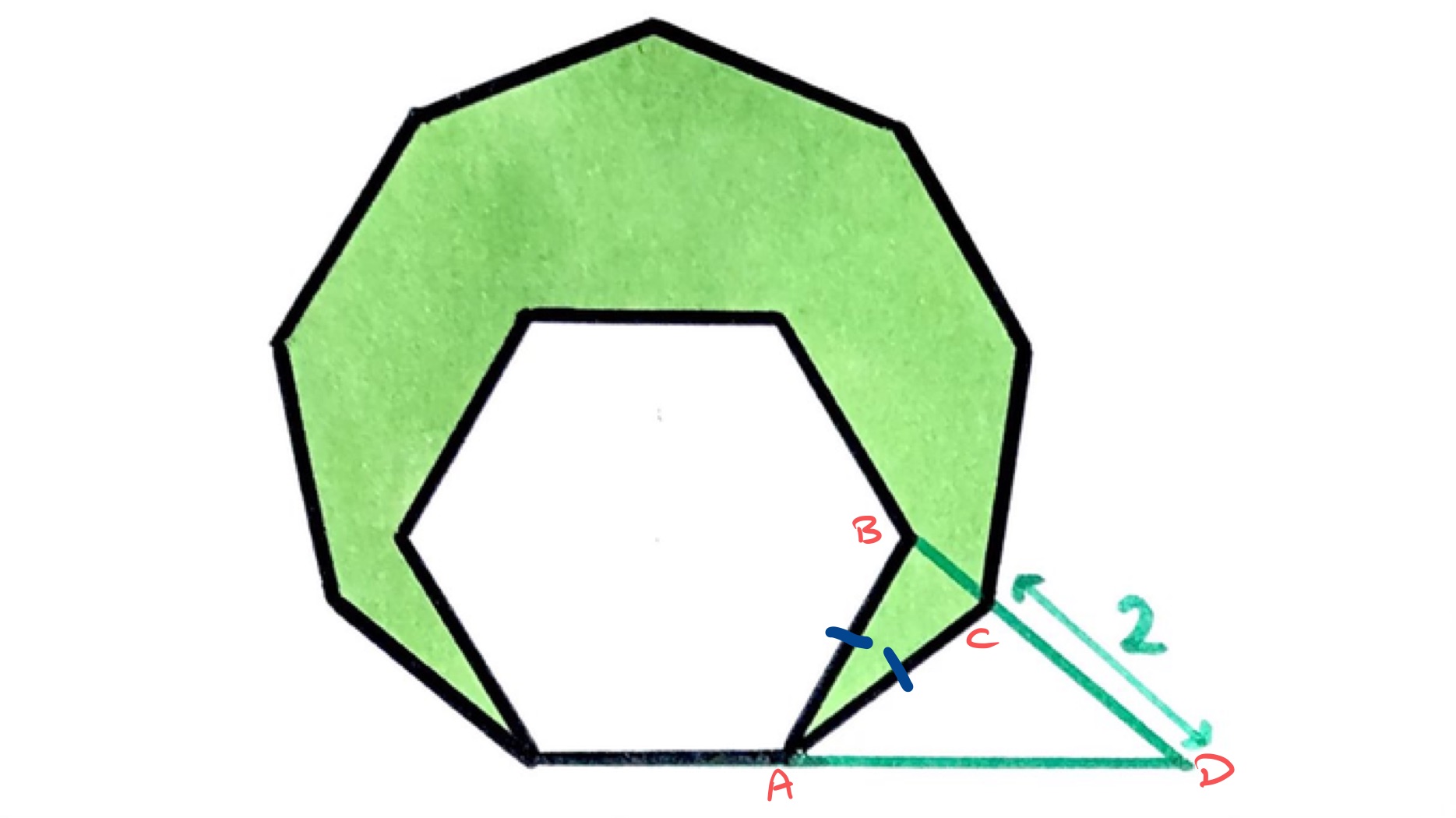
As the polygons are regular and share a side, all their sides are the same length. In particular, in the above diagram then and have the same length so triangle is isosceles. The angle at is the difference between the exterior angles of a hexagon and nonagon, which is . This means that angle and so angle since angles at a point on a straight line add up to .
Angle is the exterior angle of a nonagon, which is , so angle . This means that triangle is isosceles with and being the same length. Since has length , this means that also has length and so the side lengths of the polygons are .
The shaded area is bounded by edges from the hexagon and edges from the nonagon so its perimeter is .