Notes
stacked shapes solution
Stacked Shapes
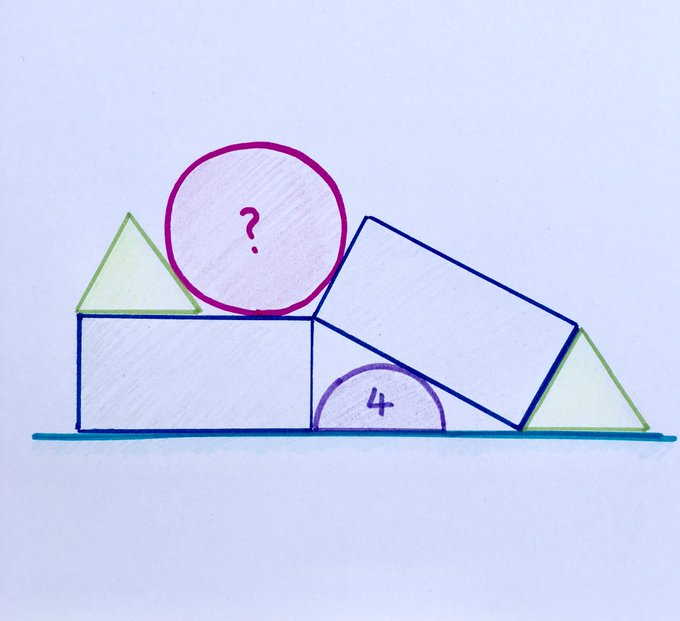
The triangles are equilateral, and the rectangles are twice as long as they are wide. If the area of the semicircle is , what’s the area of the pink circle?
Solution by Lengths in an Equilateral Triangle
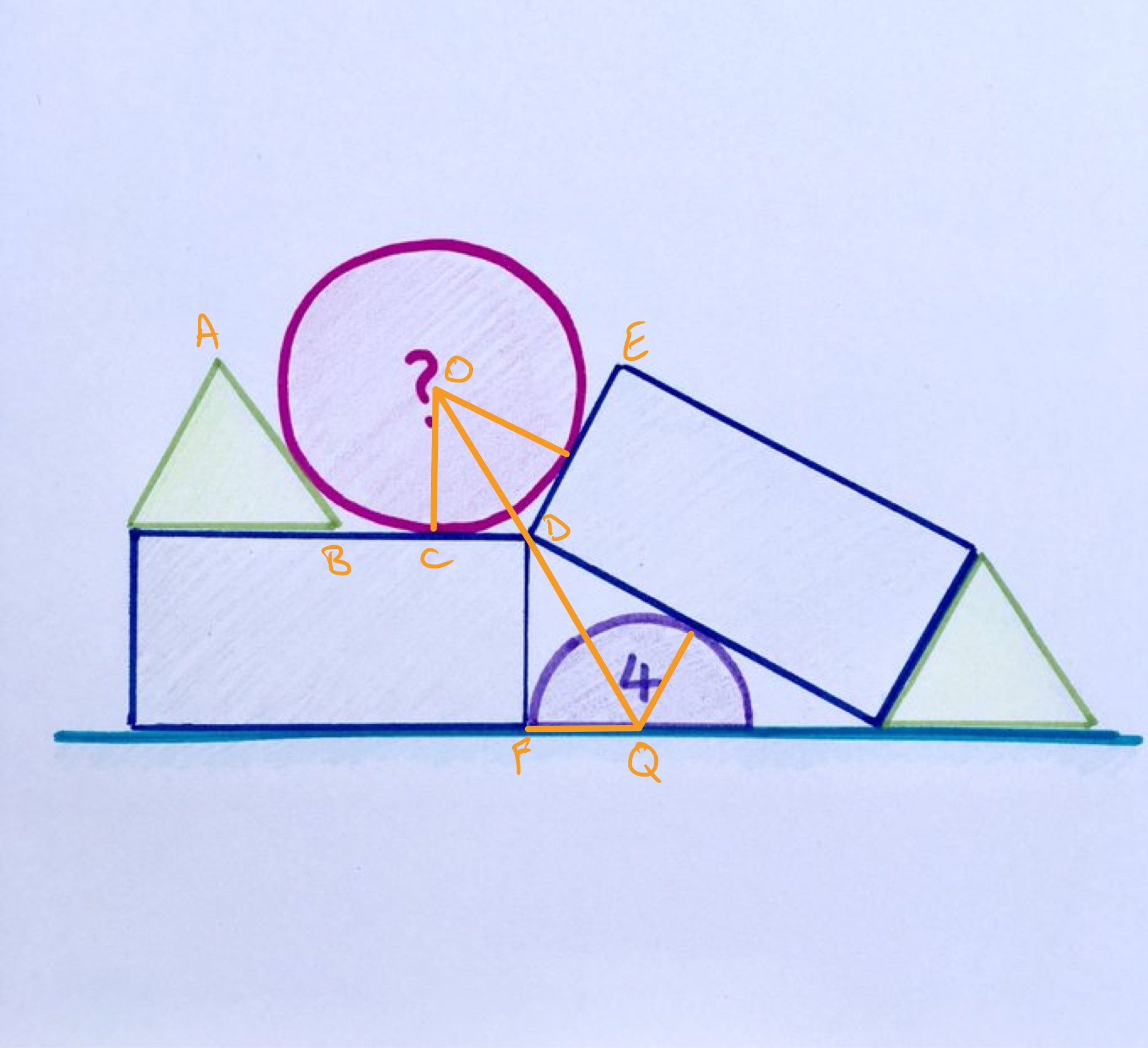
As clarified in the twitter thread, shapes of the same colour are congruent. The side of the equilateral triangle has the same length as the short side of the rectangle, and so half the length of the long side. Let be this length. Then also has length . Angles and are both the exterior angles of an equilateral triangle so are both . Angle is half that angle, so triangle is half an equilateral triangle. From the relationships between lengths in an equilateral triangle, has length . Triangle is also half an equilateral triangle, since has length , has length . The area of the semi-circle is then so . The area of the circle is therefore .