Notes
triangle over a circle solution
Solution to the Triangle Over a Circle Puzzle
Posted on Feb 17, 2021
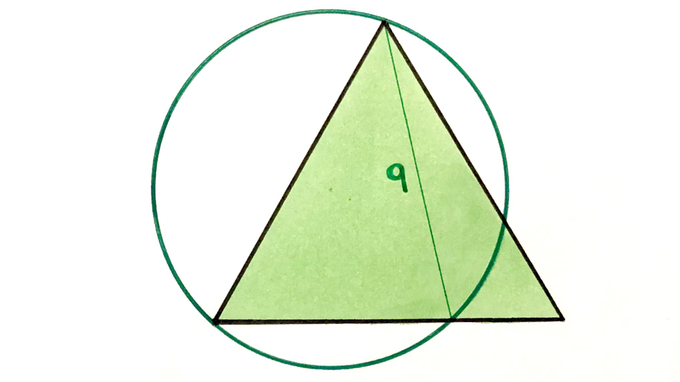
The triangle is equilateral. What’s the area of the circle?
Solution by Angles in the Same Segment are Equal and Equilateral Triangles
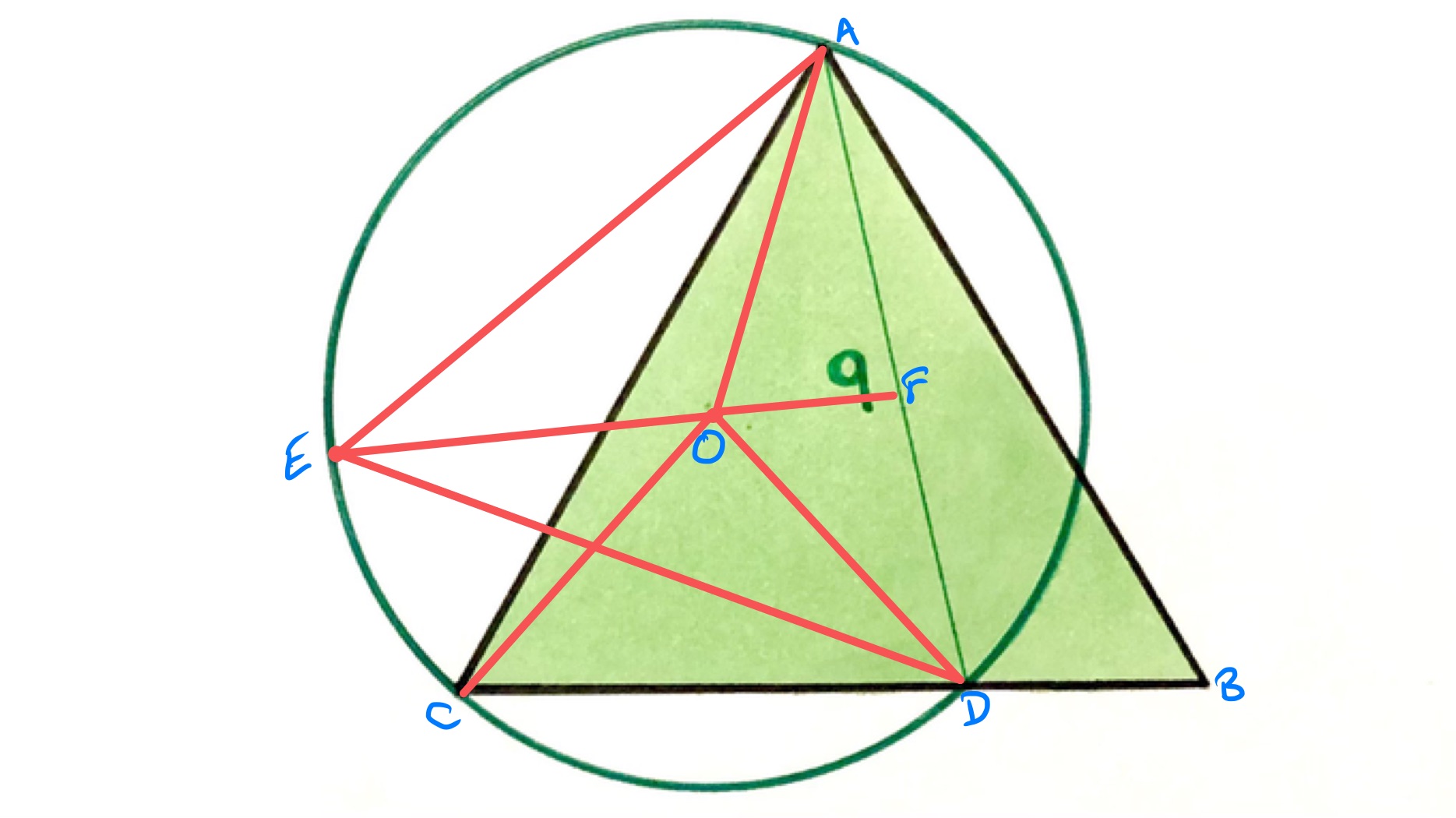
In the above diagram, point is the centre of the circle and is the point on the circumference with the property that the lengths of and are equal, so that triangle is isosceles. Point is where the line through extends to meet .
By the result that angles in the same segment are equal, angles and are equal. Since angle is the interior angle of an equilateral triangle, it is . So triangle is an isosceles triangle with an angle of and so is equilateral.
The height of an equilateral triangle is of its side length, and the centre of its circumcircle is at of its height, so the length of is of the height of triangle which is . This is the radius of the circle, and so the area of that circle is: