Notes
two circles inscribed in triangles in a semi-circle solution
Two Circles Inscribed in Triangles in a Semi-Circle
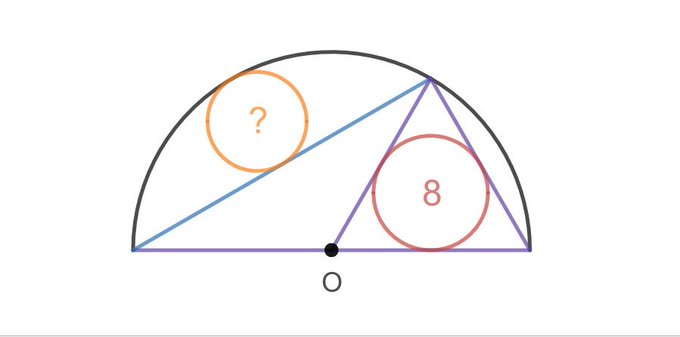
A circle of area is inscribed in an equilateral triangle. What’s the area of the other circle?
Solution by Lengths in an Equilateral Triangle
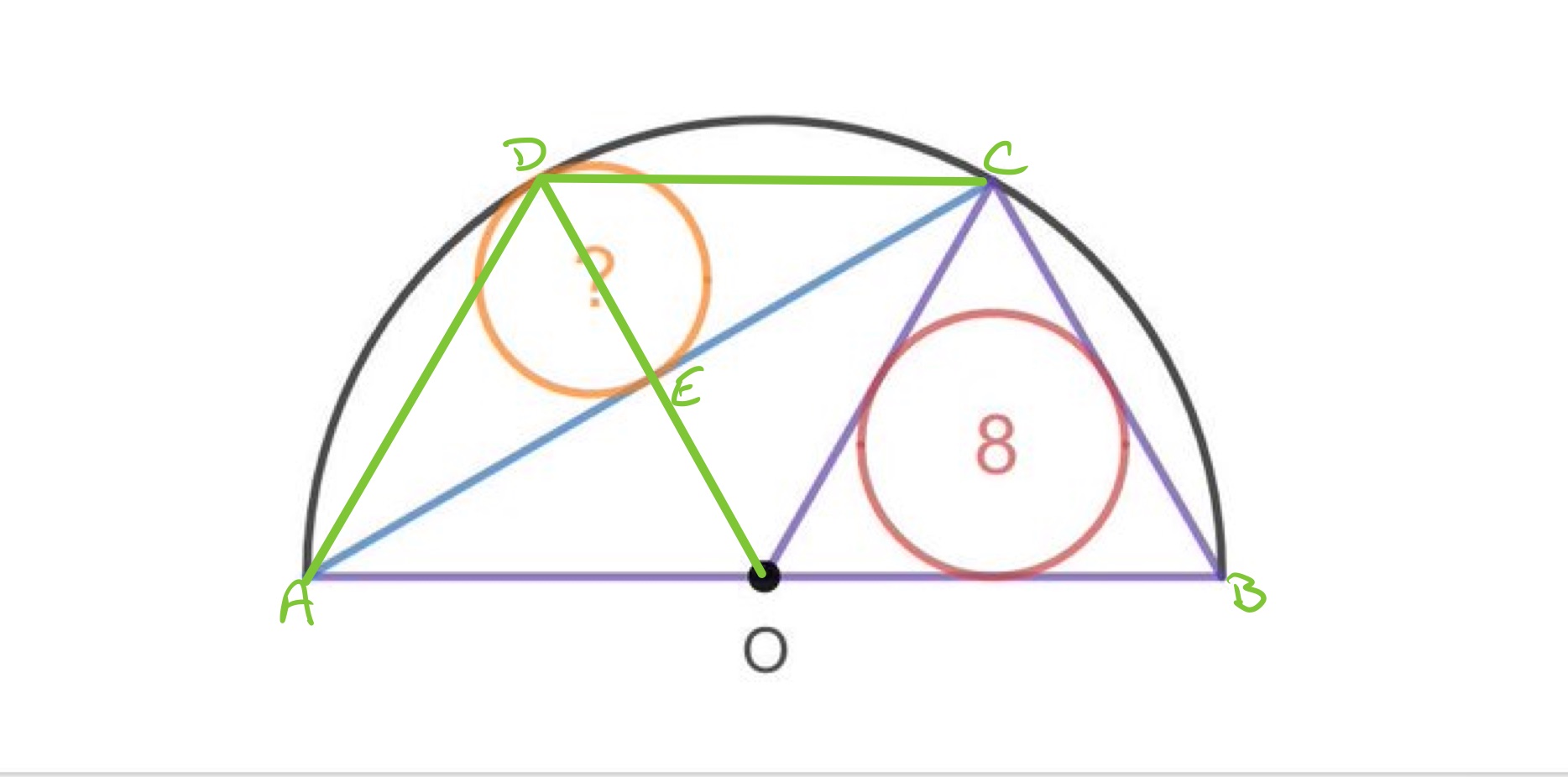
In the above diagram, let be the radius of the semi-circle, the radius of the purple circle, and the radius of the orange circle.
The line bisects , so angle is half of angle . As the angles at a point on a line add up to and the interior angle of an equilateral triangle is , angle is so angle is . Then is half an equilateral triangle, so is half of , which is , and then the radius of the smaller circle is .
From the relationships between the lengths in an equilateral triangle, the radius of the circle in the equilateral triangle is of the side length, which is . Hence , and so . Then so . Since , the area of the smaller circle is .