Notes
two squares on a hexagon solution
Solution to the Two Squares on a Hexagon Puzzle
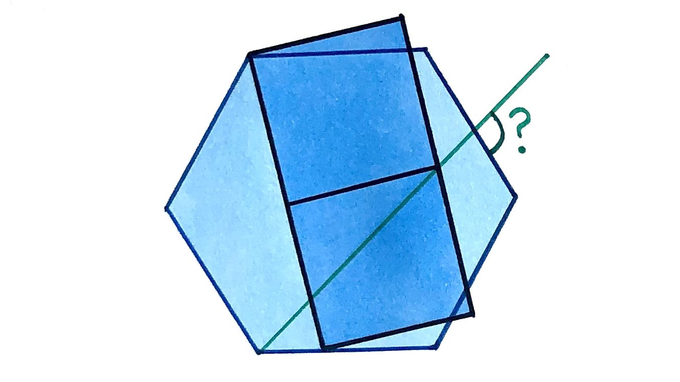
Two squares and a regular hexagon. What’s the angle?
Solution by Angle Properties
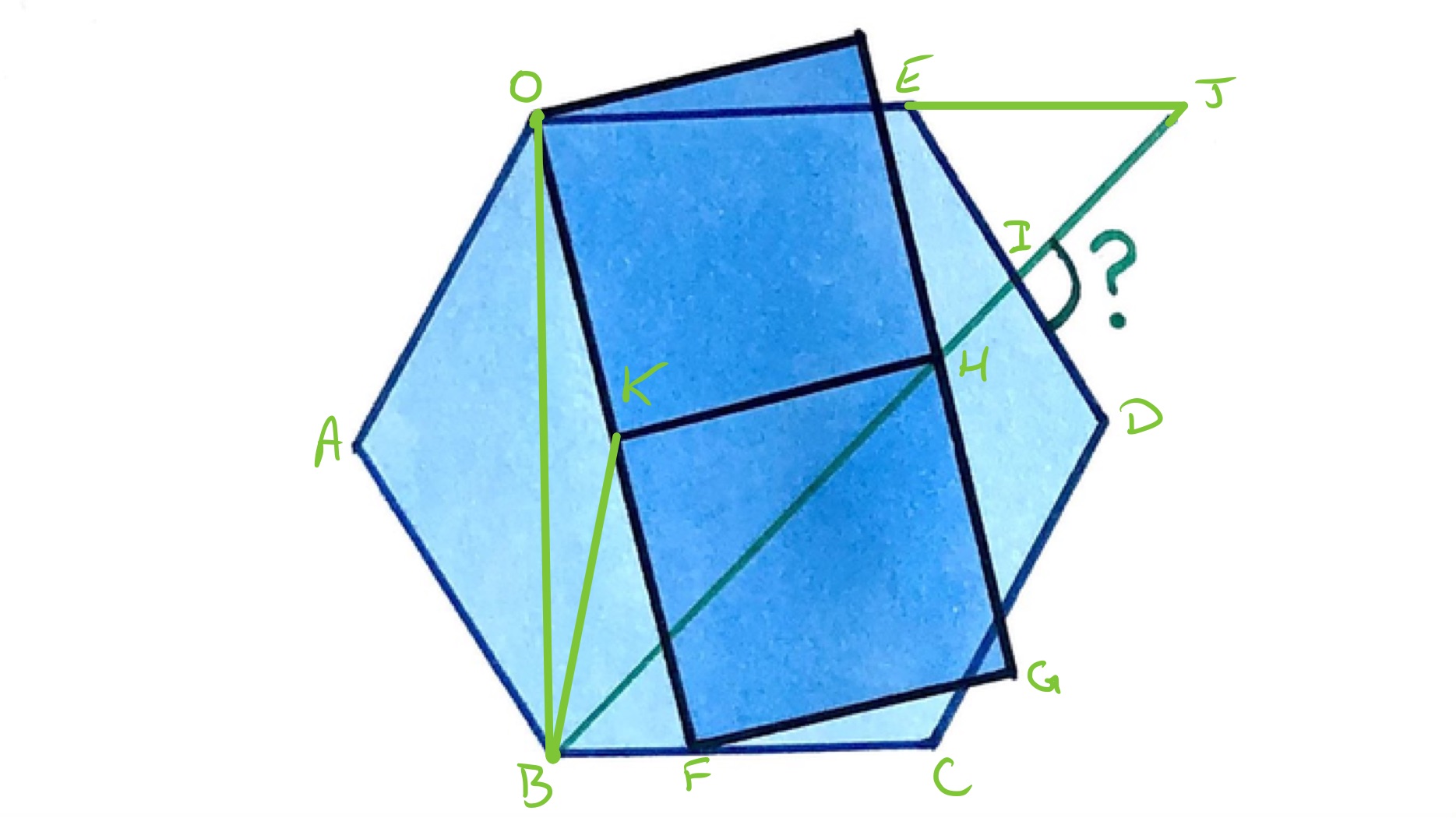
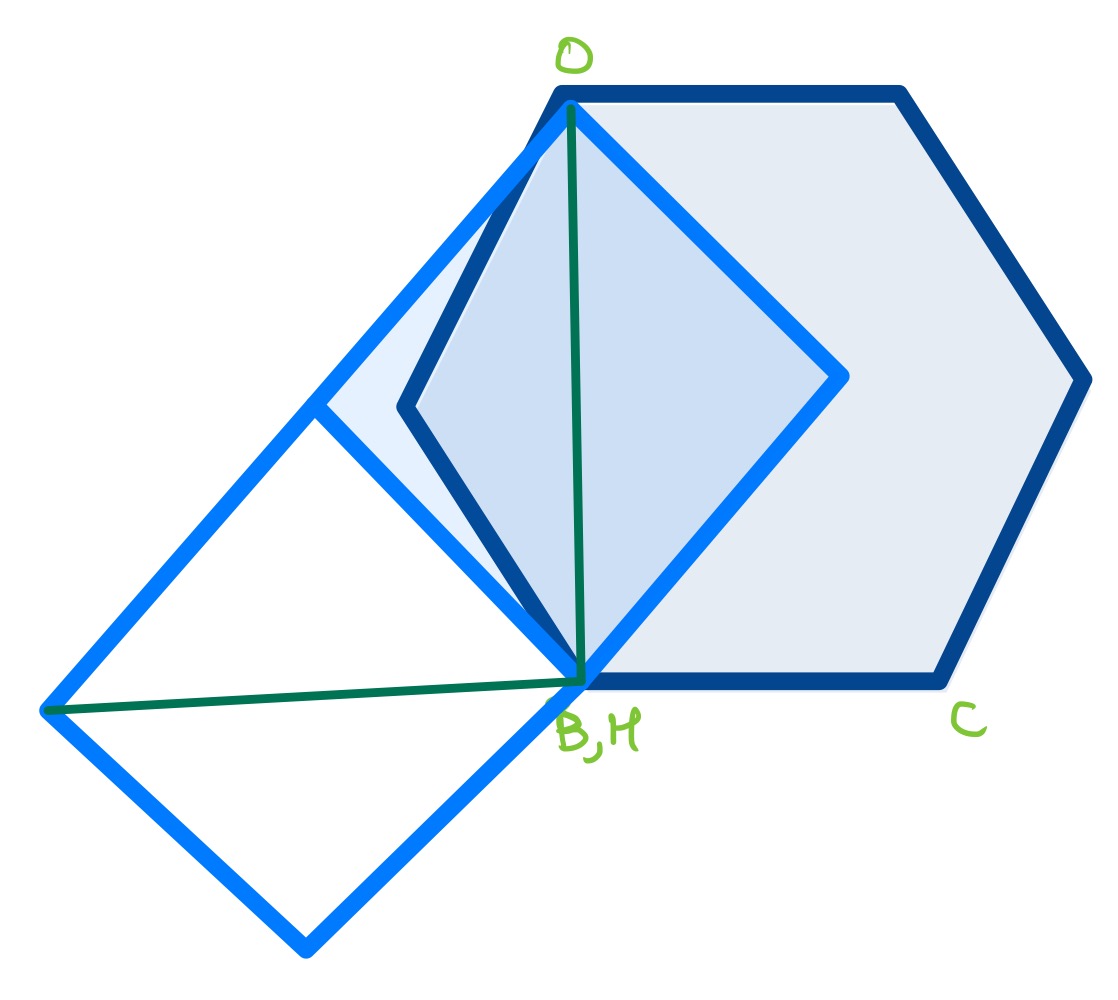
With the points labelled as above, let . Then as angle is a right angle and angles in a triangle add up to , . Since is the midpoint of and triangle is a right-angled triangle, triangle is isosceles and so angle . This means that angle and so angle .
The length of is equal to that of which is equal to the length of . Hence triangle is also isosceles and so angle is one half of which is . Then:
To get the requested angle, note that by alternate angles and as the exterior angle of a regular hexagon. So using angles in a triangle and angles on a straight line, angle .
Solution by Circle Theorems
Construct a circle centred on and passing through . As and are sides of a square, is also on this circle. As is the midpoint of , is also on this circle. Finally, as triangle is a right-angled triangle and is a diagonal, is also on this circle.
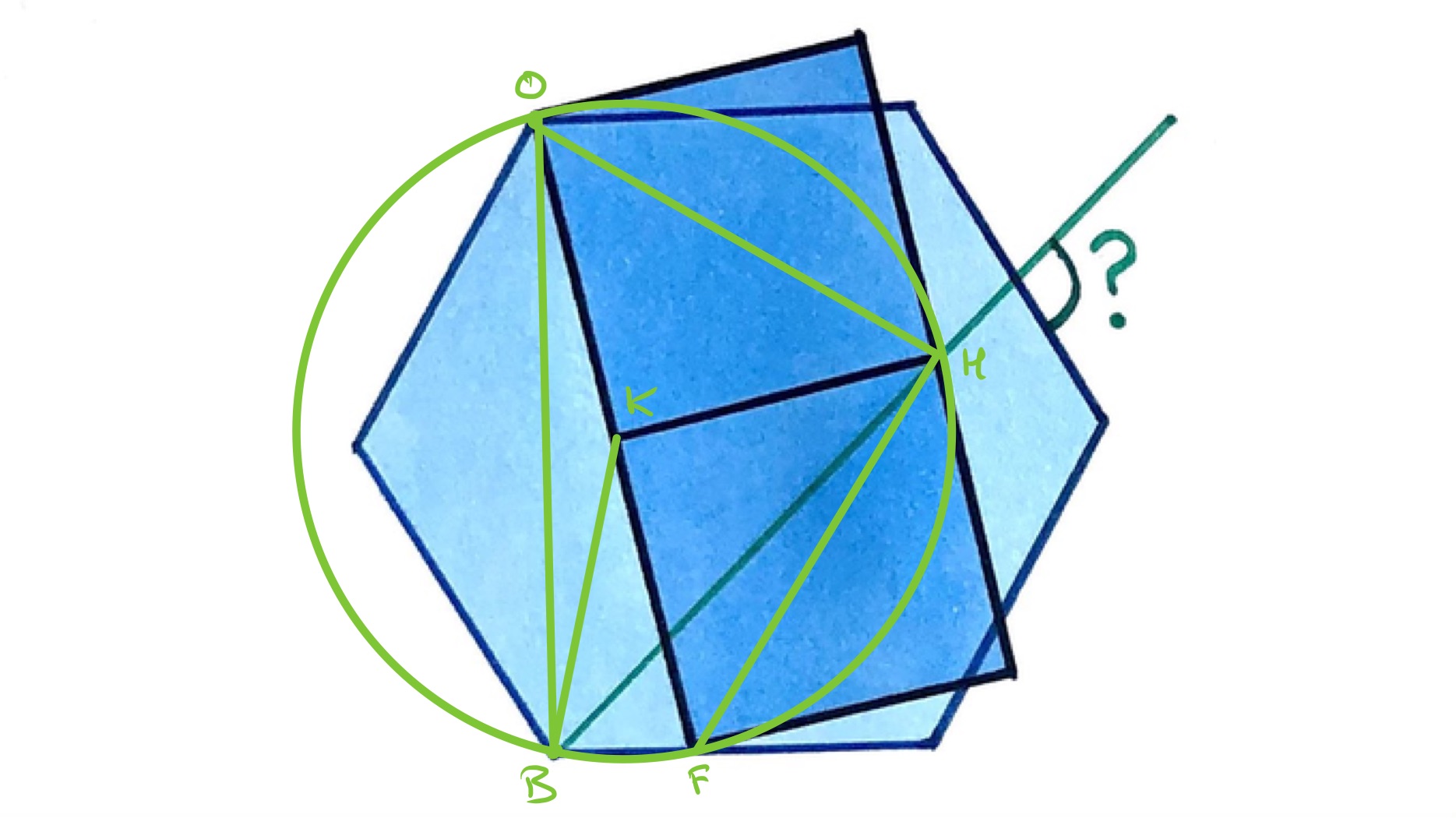
Using angles in the same segment are equal, angles and are equal. Since is the angle between a side and a diagonal of a square, it is . Hence . The requested angle then is as above.
Solution by Transformation
With the points labelled as above, the point moves on a straight line through and . The point is obtained from by a fixed transformation of a rotation of anticlockwise about and scaling by . It therefore also moves on a straight line.
To see where this straight line is, consider two special cases. In the first, is at . In this configuration, is at a point so that angle .
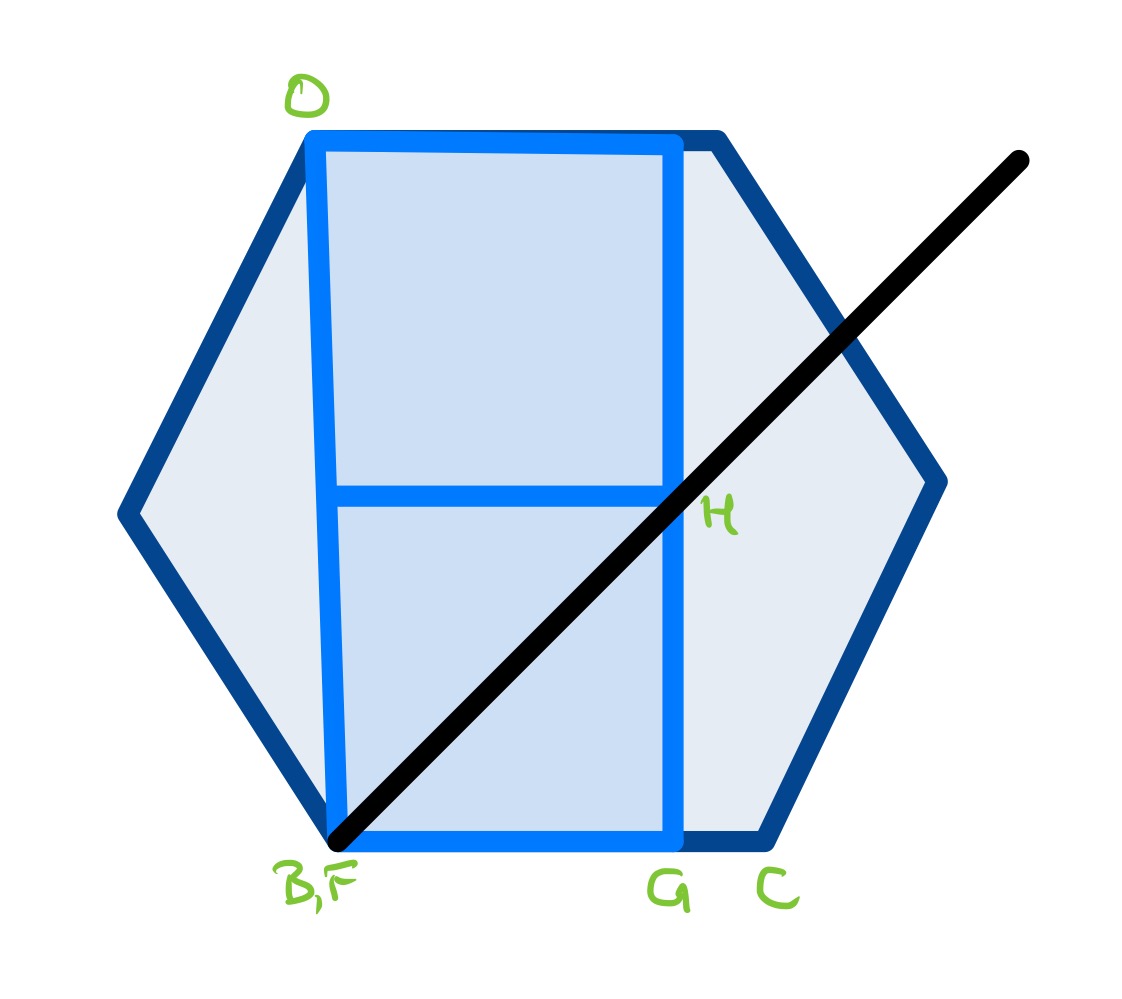
In the second, is taken to the left so that the length of is the same as that of . This brings to coincide with and shows that is on the line that moves along.
Taken together, these show that moves on a line that goes through at an angle of to the horizontal.
Solution by Invariance Principle
In the configuration where is at , the line is the diagonal of a square so the angle is . From here, the given angle can be calculated as as above.