Notes
four triangles in a square solution
Solution to the Four Triangles in a Square Puzzle
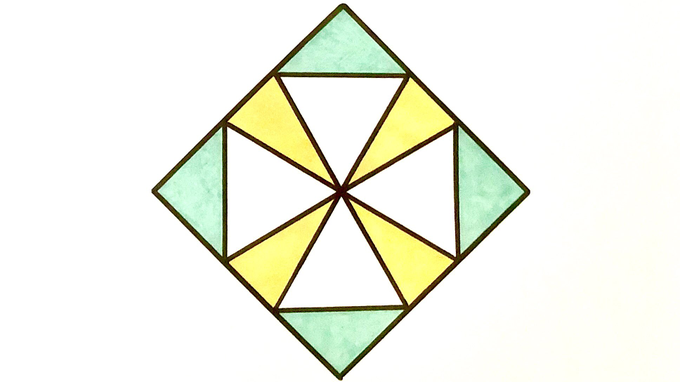
Four white equilateral triangles meet in the centre of this square. What’s the ratio of yellow to green in this design?
Solution by Areas of Special Triangles and Angle Properties
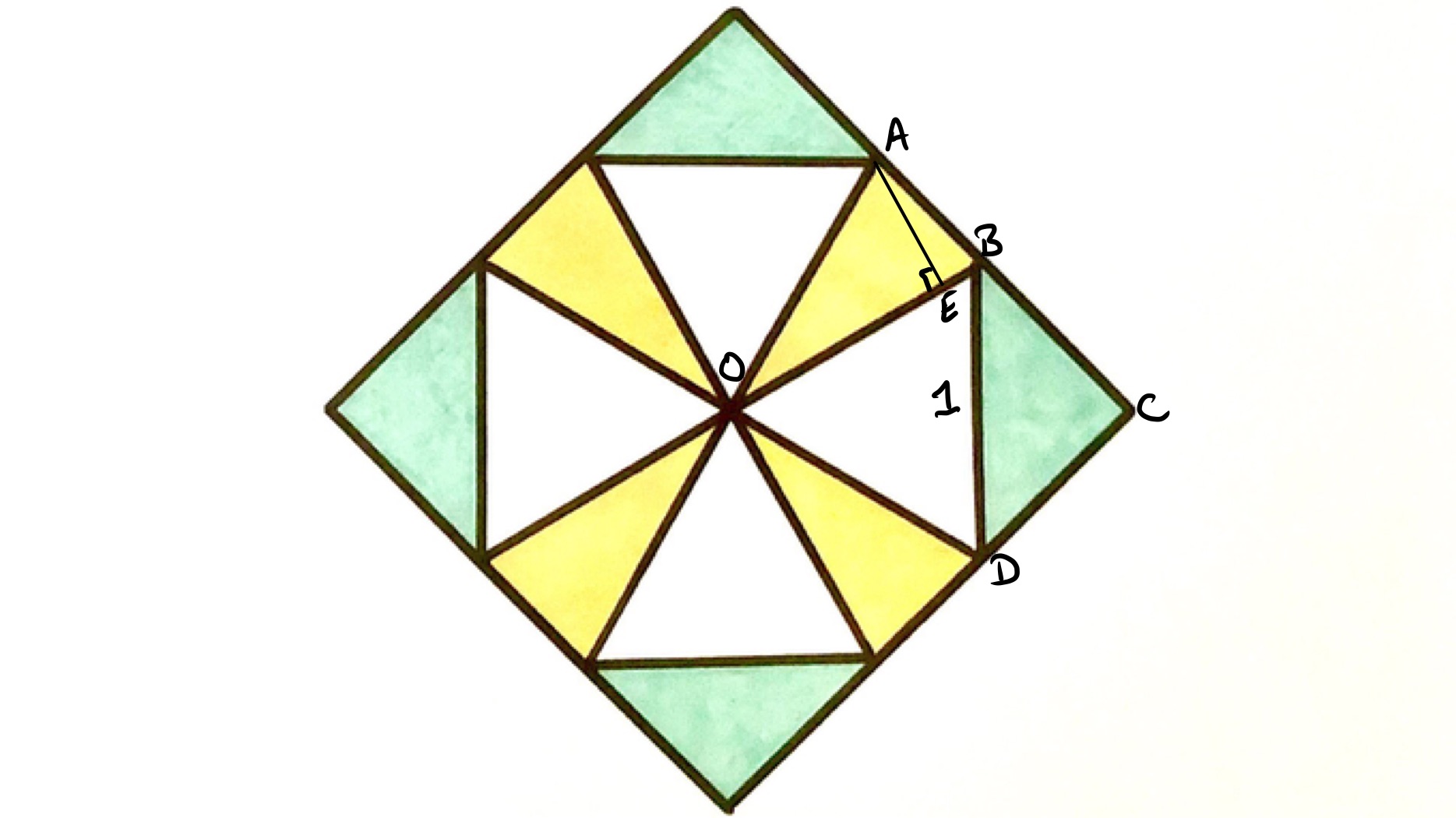
In the above diagram, triangle is equilateral so line segments and are the same length.
Triangle is isosceles and right-angled. The perpendicular distance of to the side is therefore half of the length of , so the area of this triangle is a quarter of the square of the length of .
Triangle is also isosceles. Angle is a right-angle and angle is the interior angle of an equilateral triangle, so is . This leaves angle as . In the above diagram, is the point on such that angle is a right-angle, so angle is as angles in a triangle add up to . Triangle is therefore half an equilateral triangle, meaning that has half the length of , which is the same as and . The area of triangle is therefore a quarter of the square of the length of .
Triangles and therefore have the same area and so the ratio of yellow to green in the design is .