Notes
pentagon

Pentagon

A pentagon is a polygon with five sides.

Regular Pentagon

• The exterior angle in a regular pentagon is $72^\circ$.
• The interior angle in a regular pentagon is $108^\circ$.
• The length of the line across a regular pentagon is the golden ratio times the side length.

Lengths and Angles in a Regular Pentagon

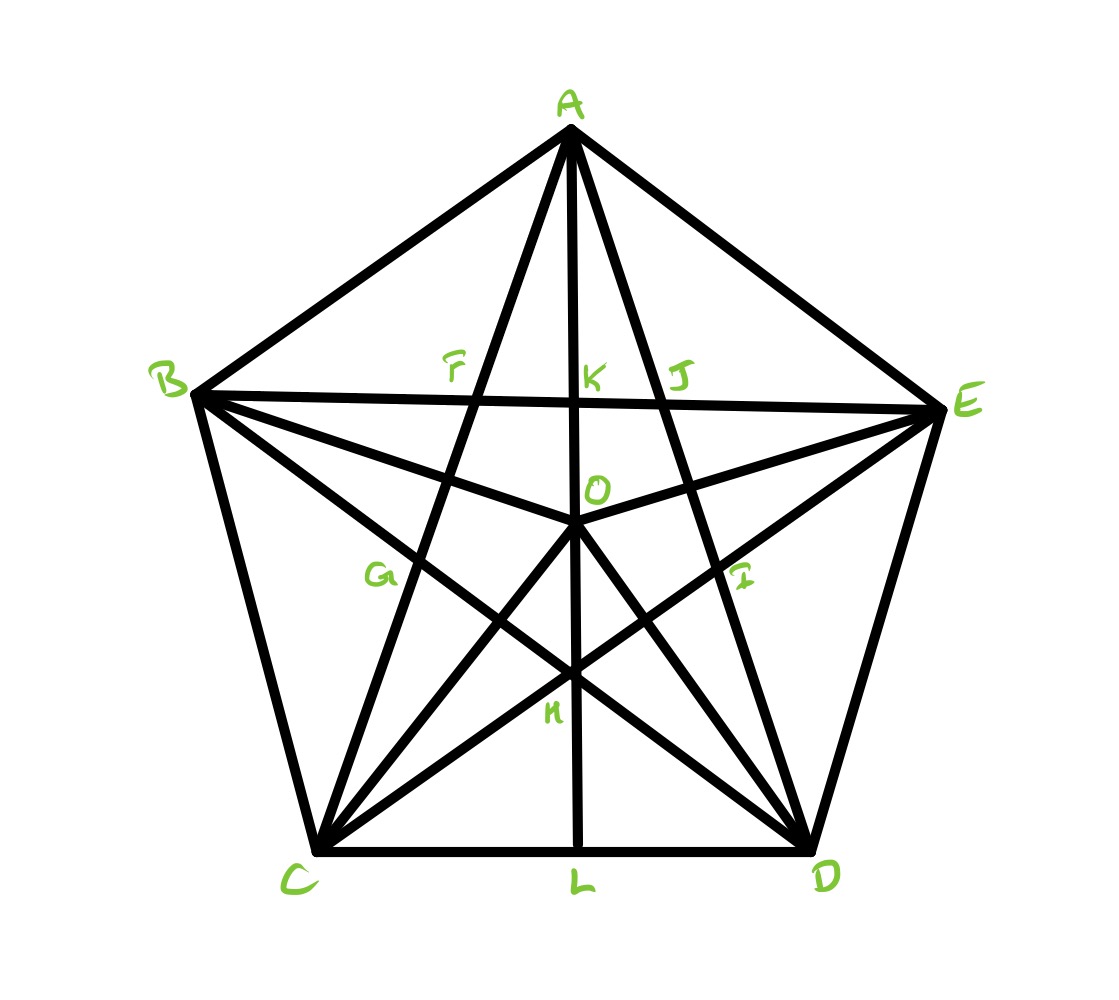
The exterior angle of a regular pentagon is $\frac{360^\circ}{5} = 72^\circ$, so the interior angle is $180^\circ - 72^\circ = 108^\circ$.

With the points labelled as in the above diagram, this means that triangle $A B E$ is an isosceles triangle with apex angle $108^\circ$ so its base angles are $\frac{180^\circ - 108^\circ}{2} = 36^\circ$. Therefore, angles $B \hat{A} F$ and $J \hat{A} E$ are both $36^\circ$, meaning that angle $F \hat{A} J = 108^\circ - 2 \times 36^\circ = 36^\circ$. So triangle $A F J$ is also isosceles with base angles $\frac{180^\circ - 36^\circ}{2} = 72^\circ$.

Triangle $A C D$ is also isosceles with angles $36^\circ$, $72^\circ$, and $72^\circ$. Then triangle $A B J$ has angles $J \hat{B} A = 36^\circ$, $B \hat{A} J = 108^\circ - 36^\circ = 72^\circ$, and angle $A \hat{J} B = 72^\circ$ so is also isosceles. These three triangles are therefore all similar, and the scale factors are such that the short side of $A C D$ has the same length as the long sides of $A B J$, and the short side of $A B J$ has the same length as the long sides of $A F J$.

Let $a$ be the length of $F J$, and let $\phi$ be the length scale factor from $A F J$ to $B J A$, so then $A F$ has length $\phi a$, and $A B$ has length $\phi^2 a$. Since $A B J$ is isosceles, $A B$ and $B J$ have the same length, and this is equal to the lengths of $B F$ and $F J$ which is $\phi a + a$. Hence $\phi^2 a = \ph a + a$, or equivalently $\phi^2 = \phi + 1$. Together with the condition that $\phi \gt 1$, this establishes $\phi$ as the golden ratio.

Now consider the two radii of the pentagon: the radius of the incircle and the circumcircle, equivalently the lengths of $O L$ and $O D$. Write these as $r$ and $R$, respectively. Let $b$ be the side length of the pentagon. Viewing $C D$ as the base of triangle $C D O$, its area is $\frac{1}{2} b r$. Viewing $O D$ as its base, its height is half the length of $C E$ which is $\phi b$ so its area is $\frac{1}{4} \phi b R$. Equating these establishes that $2 r = \phi R$.

Lastly, the total height of the pentagon, which is the length of $A L$, relates to the side length via Pythagoras' theorem applied to the triangle $A L C$. The length of $C L$ is half a side-length, $\frac{1}{2} b$, and the length of $A C$ is $\phi b$. So $A L$ has length: