Notes
regular hexagon and rectangle solution
Solution to the Regular Hexagon and Rectangle Puzzle
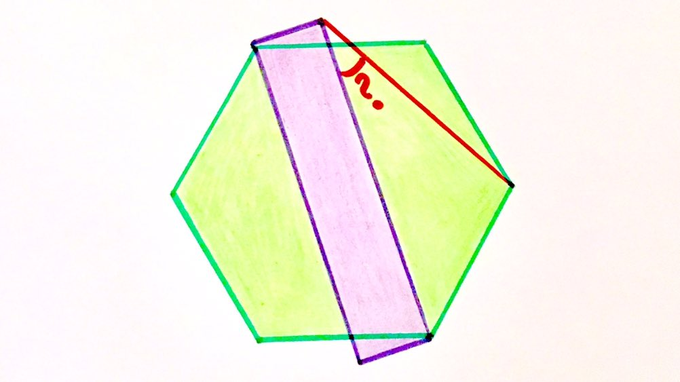
Here’s a regular hexagon and a rectangle. What’s the angle?
Solution by Angle at the Circumference is Half the Angle at the Centre
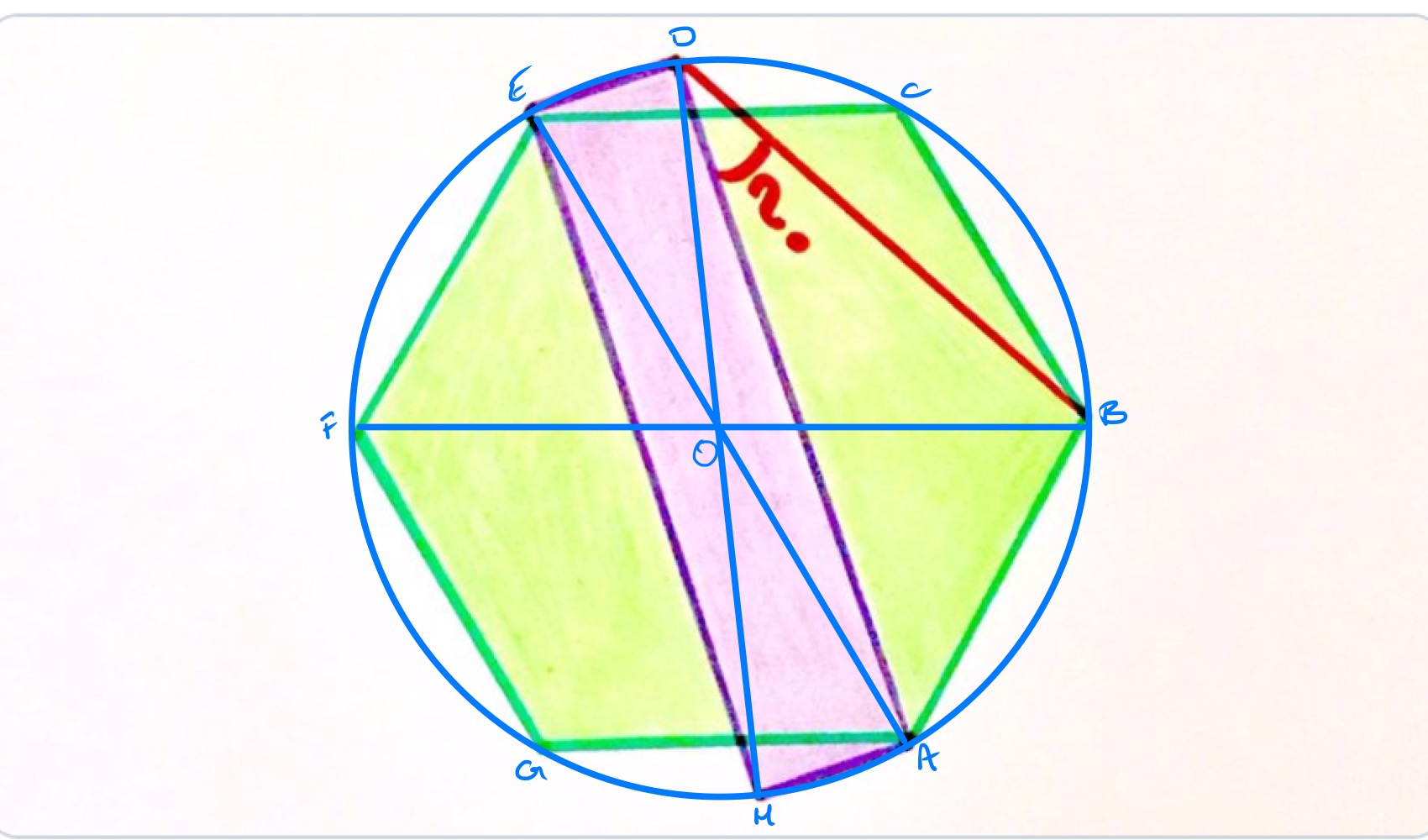
The circle in the above diagram is the circumcircle through the vertices of the hexagon and the point labelled is its centre. This is also the centre of the rectangle and so the vertices of the rectangle also lie on the circle. The angle is then half of angle since the angle at the circumference is half the angle at the centre. Triangle is an equilateral triangle as it is formed from the regular hexagon so angle is meaning that angle is .
Solution by Invariance Principle
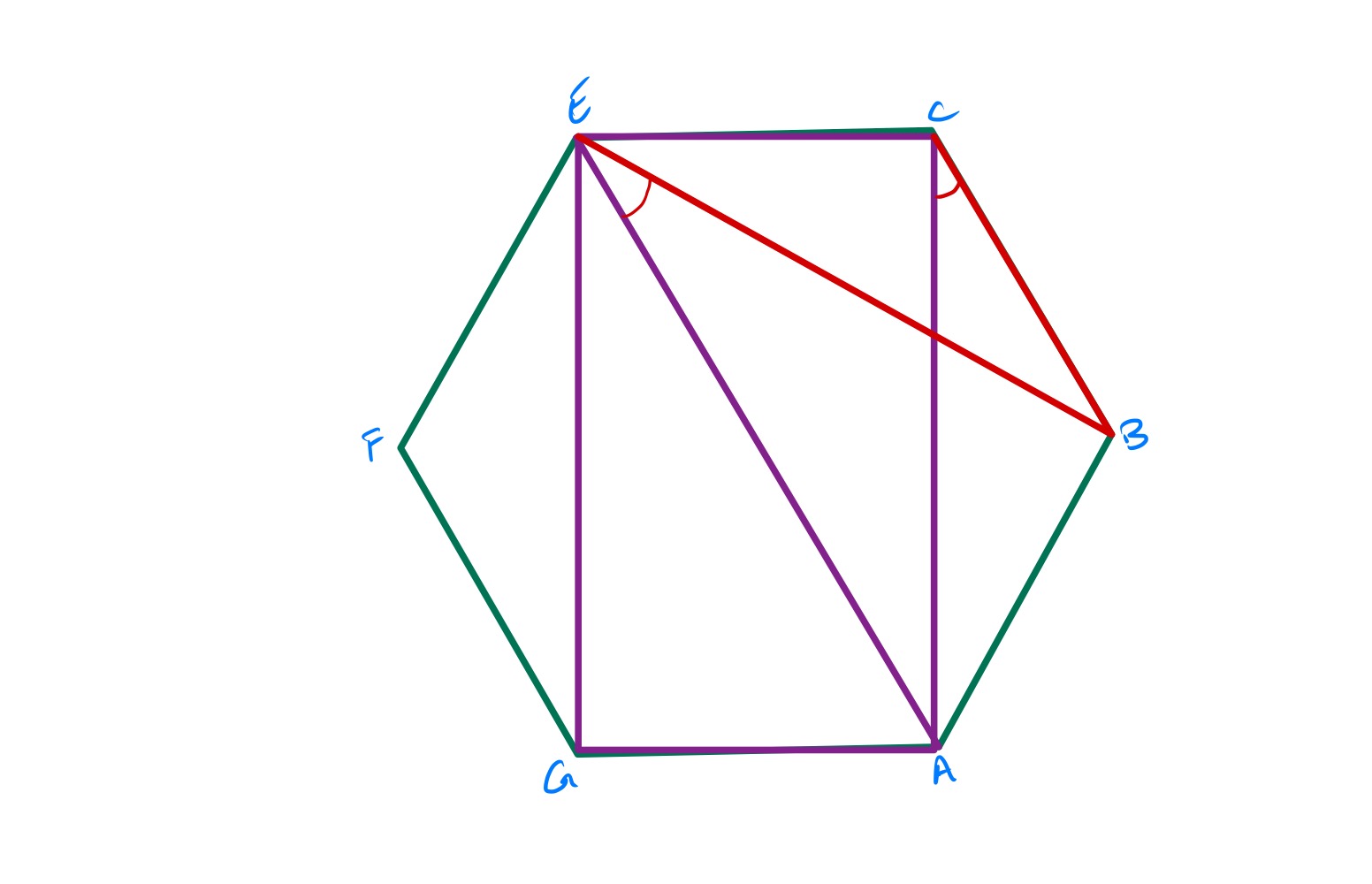
Under the assumption that the angle doesn’t depend on the size of the rectangle (providing it shares a diagonal with the hexagon) there are two configurations where the angle can be easily deduced. These are both shown in the above diagram. In one, the rectangle is viewed as actually being the line so the angle in question is . In the other, the rectangle is so the angle in question is .
Triangle is isosceles and angle is the interior angle of a regular hexagon so is , meaning that angle is . Then angle is also , while angle is , meaning that angle is .