Notes
isosceles and equilateral triangles solution
Solution to the Isosceles and Equilateral Triangles Puzzle
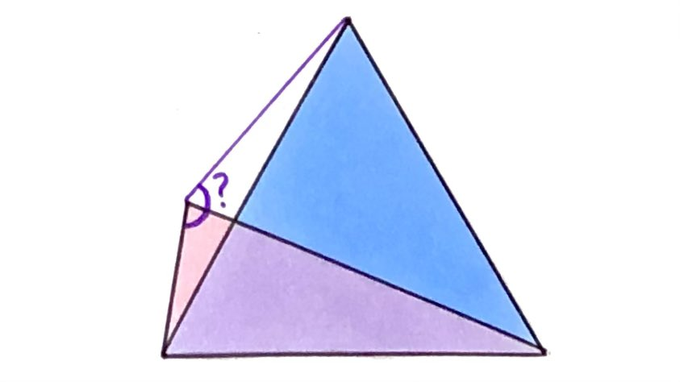
A blue equilateral triangle overlaps a pink isosceles triangle. What’s the angle?
Solution by Direct Calculation
Consider the labelled diagram.
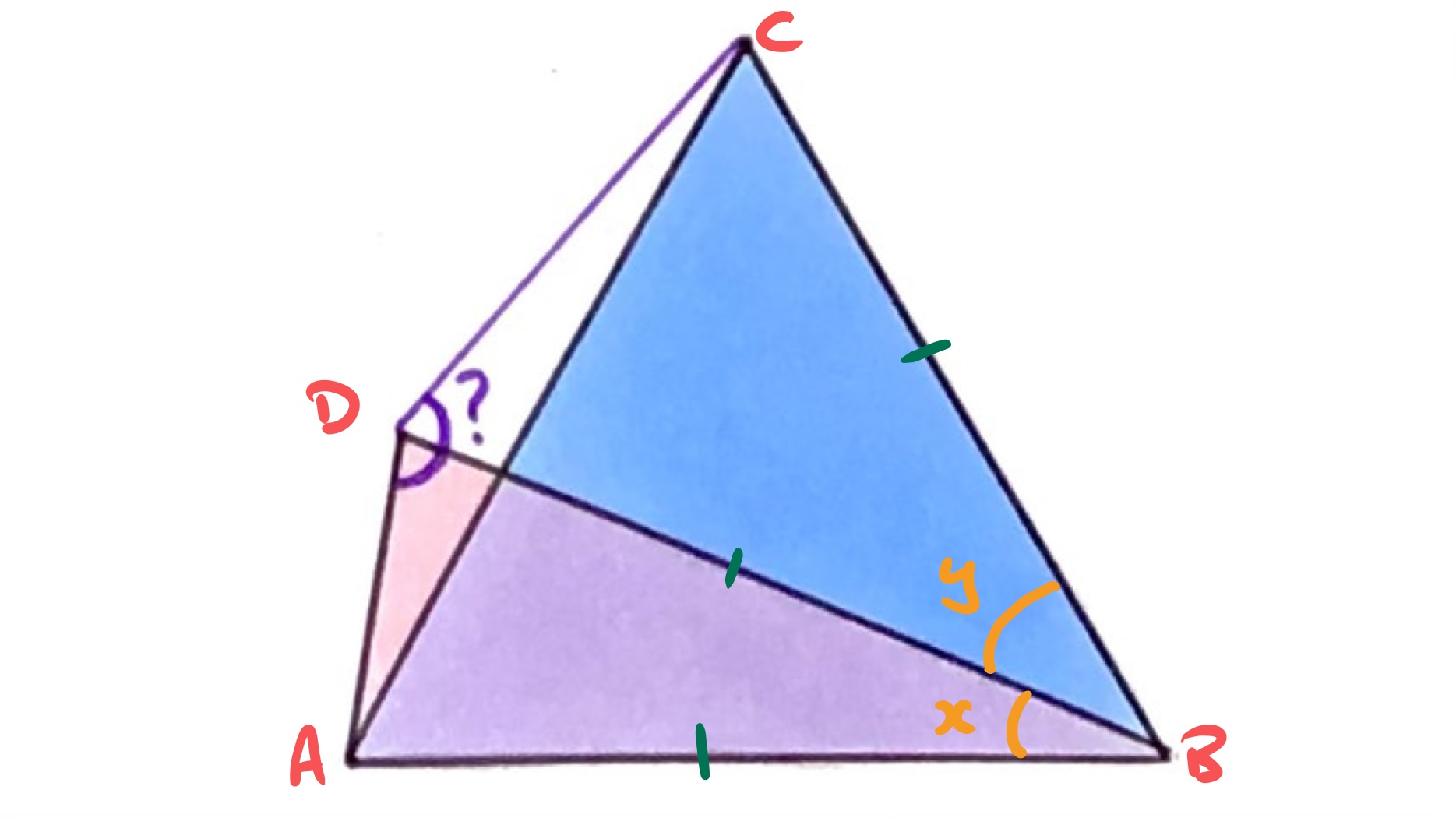
Let and . Then as the interior angle in an equilateral triangle.
As triangle is isosceles, angle is half of . Also, as it is isosceles then , then as triangle is equilateral, so triangle is also isosceles. By the same reasoning, then, angle is half of . Putting these together, angle is:
Solution using Circles
Since triangle is isosceles and is equilateral, drawing a circle centred on with radius passes through both and .
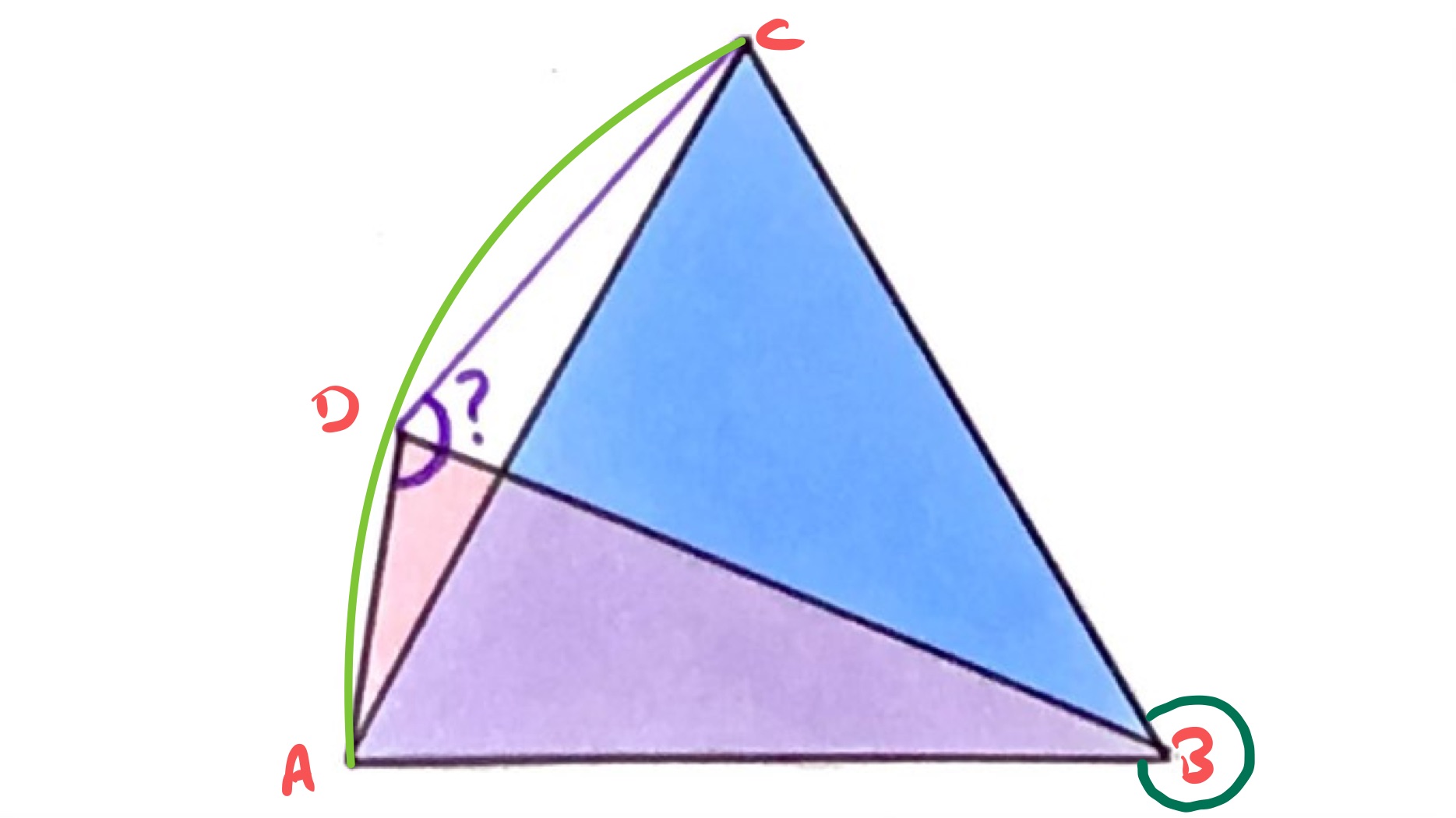
Using the angle on the circumference is half the angle at the centre then angle is half of angle , where the latter is the reflex angle. Hence: