Notes
two squares inside an equilateral triangle solution
Two Squares Inside an Equilateral Triangle
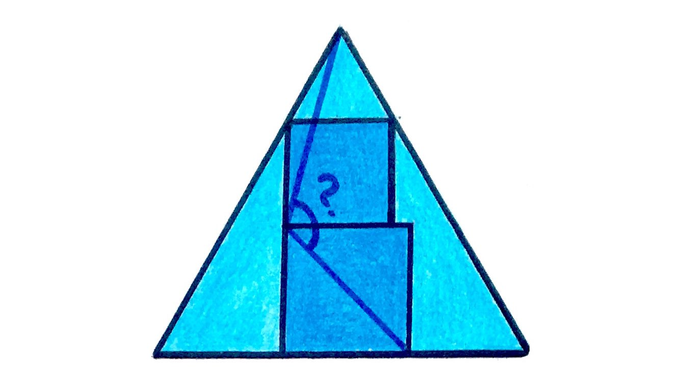
Two squares inside an equilateral triangle. What’s the angle?
Solution by Interior Angles of Regular Polygons
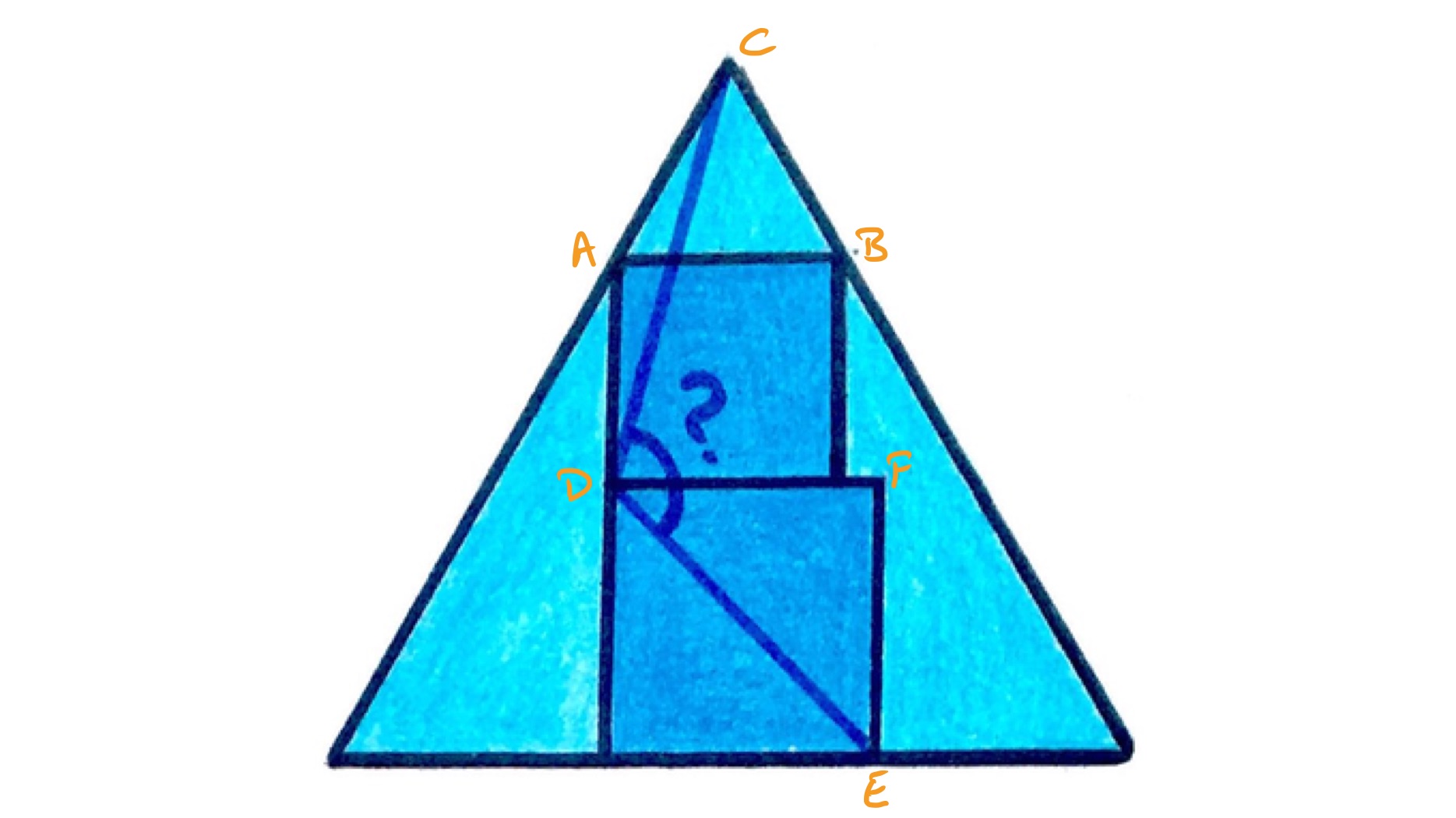
The line segment is parallel to the base of the equilateral triangle, so triangle is also equilateral. Therefore, line segments and are of equal length, so triangle is isosceles. The angle is as it is formed from interior angles in regular polygons, so angle is . This leaves for angle and so angle is .