Notes
trapezium

Trapezium

A trapezium is a quadrilateral in which two sides are parallel.

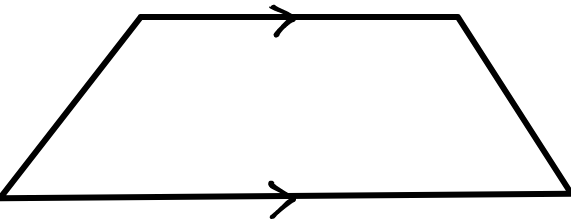
Writing $a$ and $b$ for the lengths of the parallel sides and $h$ for the perpendicular distance between them then the area of a trapezium is given by the formula:

There are various ways to see that this is true. One is to take two trapeziums and place them alongside each other to make a parallelogram. The area of the parallelogram is $(a + b)h$, and the trapezium is half of that.

Crossed Trapezium

A crossed trapezium is a trapezium together with its diagonals. The four triangles formed by drawing in the diagonals have special properties. The two triangles which include the parallel sides are similar while the other two triangles have the same area.

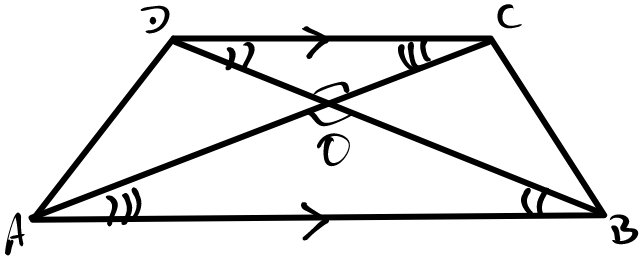
In this picture, $C\hat{A}B = D \hat{C } A$ as they are alternate angles, similarly $D \hat{ B} A = B \hat{ D } C$. So triangles $A O B$ and $C O D$ are similar.

To see that the side triangles are the same area, note that triangles $A D B$ and $A C B$ have the same base and same perpendicular height so have the same area. Both consist of a side triangle together with triangle $A O B$, and hence the two side triangles have the same area.

The areas of the four triangles are related by the scale factor between the similar triangles. Let $s$ be the (linear) scale factor from $C O D$ to $A O B$. Then $A O = s O C$. Triangles $A O D$ and $D O C$ have the same height and their bases are, respectively, $A O$ and $O C$. We therefore have that the area of $A O D$ is $s$ times that of $D O C$. Similarly, the area of $A O B$ is $s$ times that of $A O D$.

This means that the total area of the trapezium is $1 + s + s + s^2 = (1 + s)^2$ times the area of $DOC$.