Notes
quartered hexagon solution
Solution to the Quartered Hexagon Puzzle
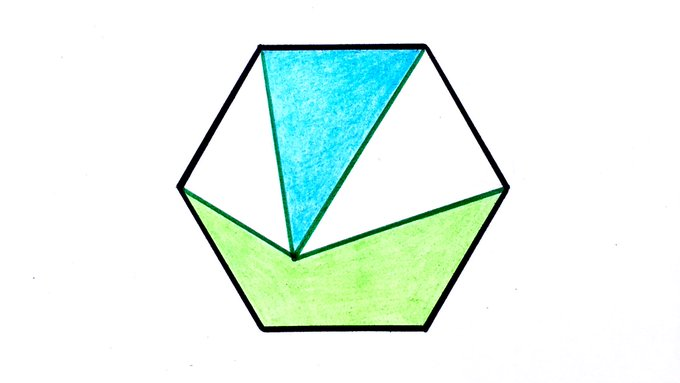
Quarter of this regular hexagon is blue. What fraction is green?
Solution by Properties of Regular Hexagons and Equilateral Triangles, and Areas of a Triangle and a Trapezium
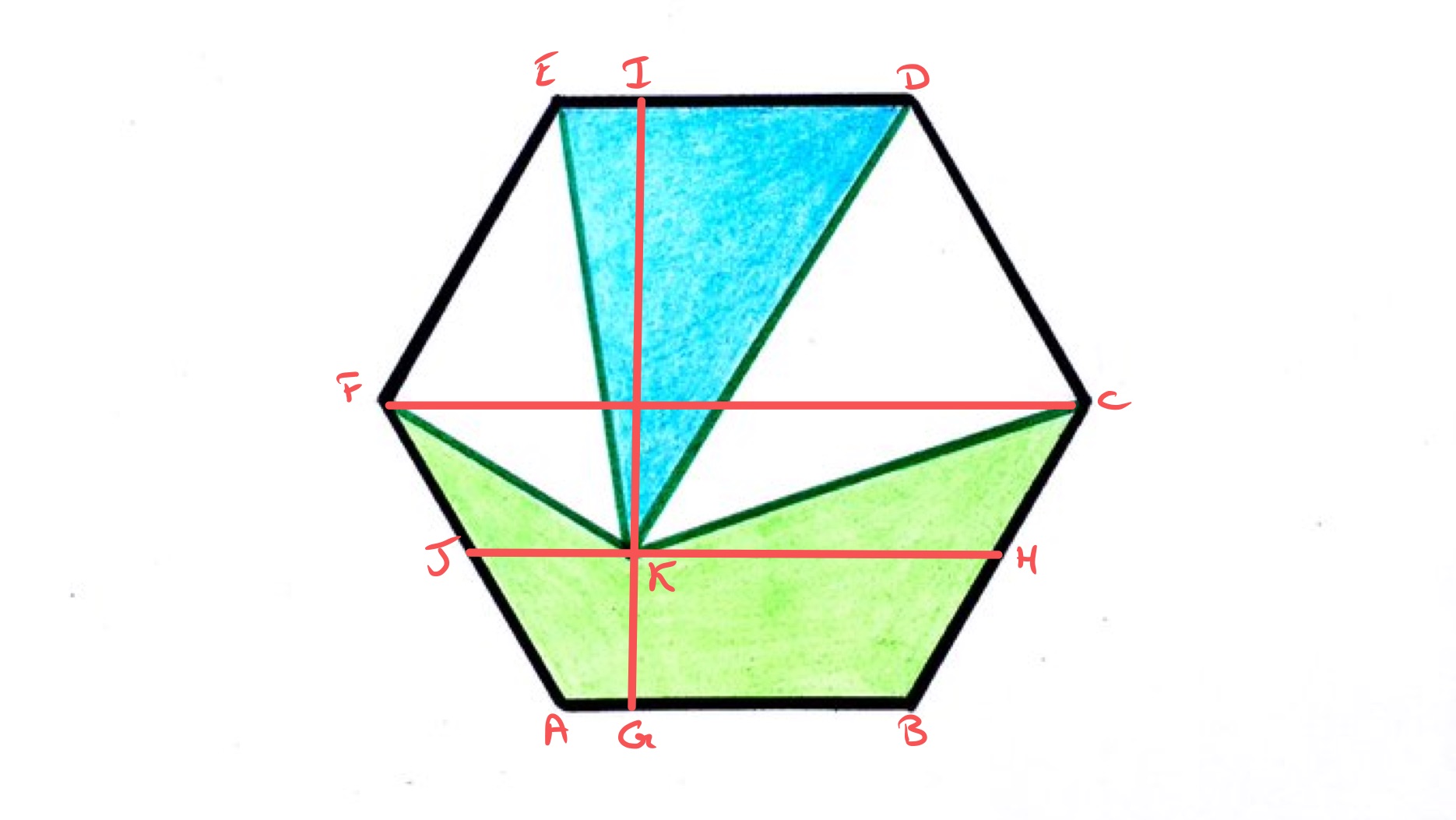
In the above diagram, the line is horizontal and passes through , while is vertical and likewise through .
The regular hexagon decomposes into six equilateral triangles with the same side length as the hexagon. Therefore, the area of one of these triangles is a sixth of the area of the full hexagon. The height of one of these triangles is the perpendicular distance from the centre to a side, which is half the length of . So a triangle with base and full height the length of has area one third of the hexagon. Since has area one quarter of the hexagon, the length of must be of the length of .
The green area can then be decomposed in different ways to calculate its area, but ultimately they end up comparing it to the trapezium with area half that of the hexagon. Writing for the side length of the hexagon and for the perpendicular distance between and then the area of the trapezium is so represents a third of the hexagon.
Slicing the green region along splits it into a trapezium and two triangles. The length of is and of is so the area of the trapezium is . The two triangles have height and their combined base is so their combined area is . The green region thus has total area which, as established above, is a third of the hexagon.
An alternative decomposition is to view the green region as being half the hexagon with triangle removed. With as its “base”, this triangle has base and height so its area is . Its area is therefore one sixth of the hexagon so the green area is one third.
Solution by Invariance Principle
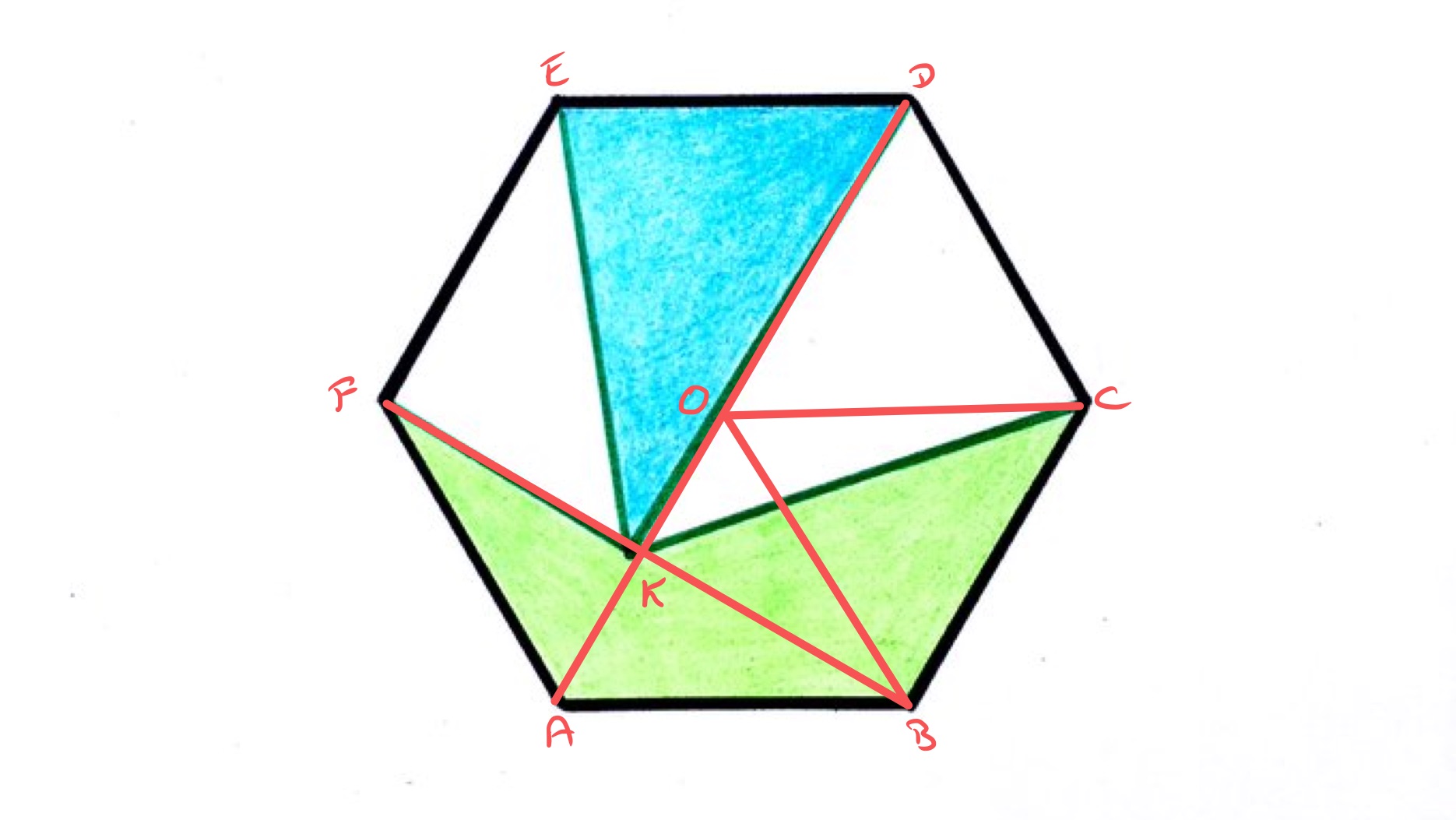
The point in the diagram can be anywhere in the hexagon provided triangle occupies a quarter of the total area. There is a possible configuration where lies on the diagonal , since if is at then the blue triangle is a third of the hexagon while if is at (the centre) then the blue triangle is a sixth.
With on the line then the triangle has the same area as since both have the same “base” and the same “height” above this base. Therefore, triangle is one sixth of the hexagon. Triangle is also one sixth, so the area of the green region is one third of the area of the hexagon.