Notes
two triangles in a circle and semi-circle solution
Solution to the Two Triangles in a Circle and Semi-Circle Puzzle
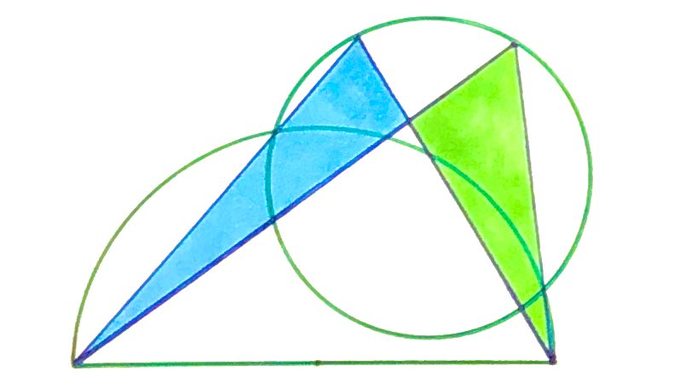
Which of the shaded triangles has the largest area?
Solution by Cyclic quadrilateral, Angles at a point on a straight line, and Crossed trapezium
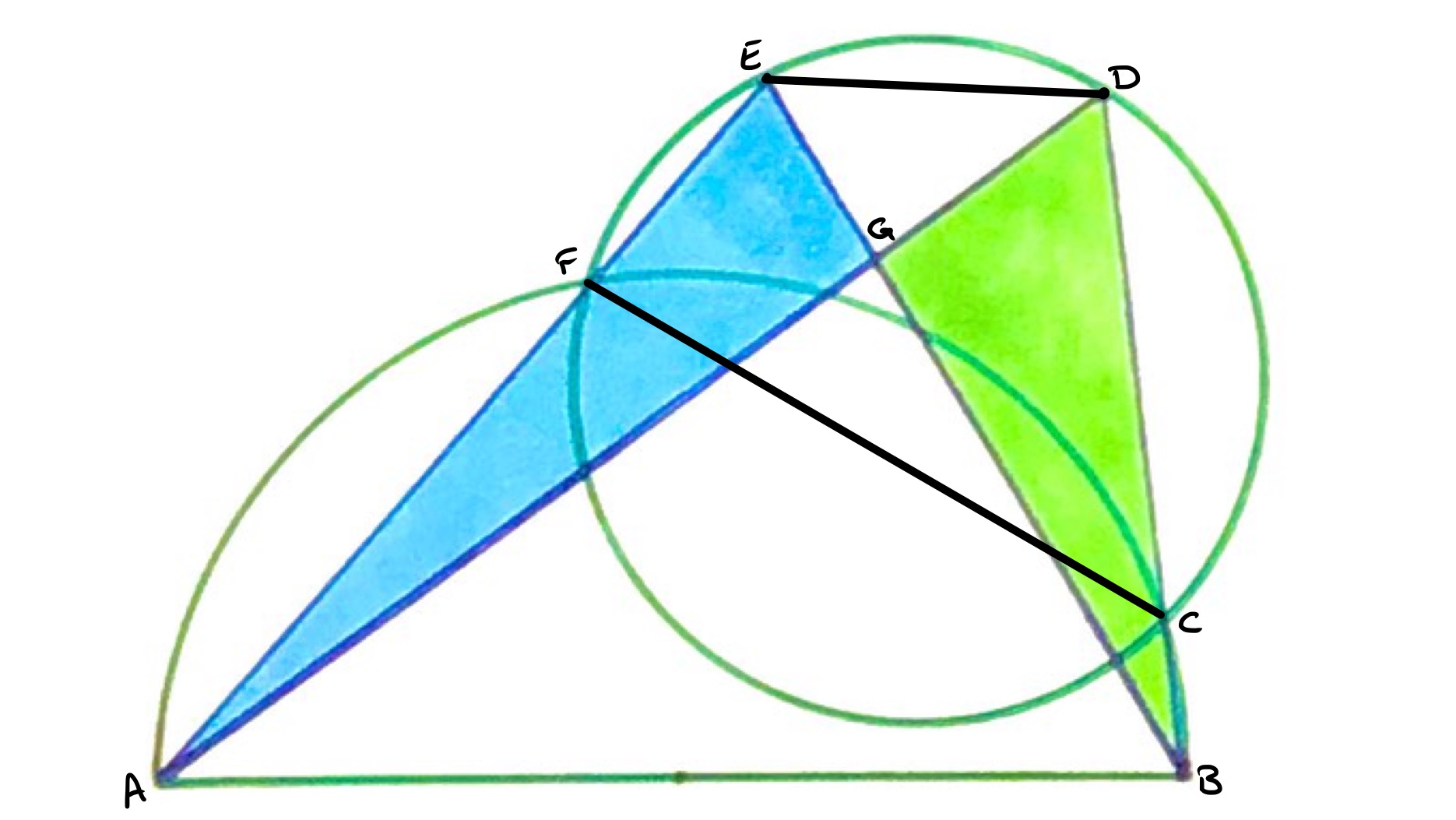
In the above diagram, quadrilateral is cyclic (in the semi-circle) and so angles and add up to (that is, are supplementary). For the same reason, angles and also add up to . Since angles at a point on a straight line add up to , angles and add up to . Putting all those together, angles and add up to . This establishes and as parallel and so quadrilateral is a trapezium.
As detailed at crossed trapezium, the two triangles therefore have the same area.