Notes
circle in a trapezium solution
Solution to the Circle in a Trapezium Puzzle
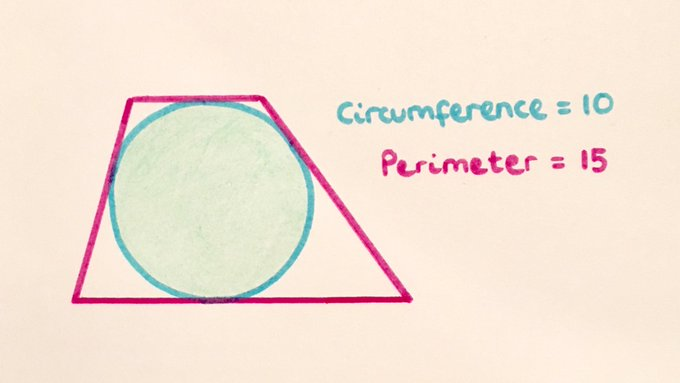
What fraction of the trapezium is shaded?
Solution by Congruent Triangles, Angle Between a Radius and Tangent, Area of a Trapezium, and Area of a Circle
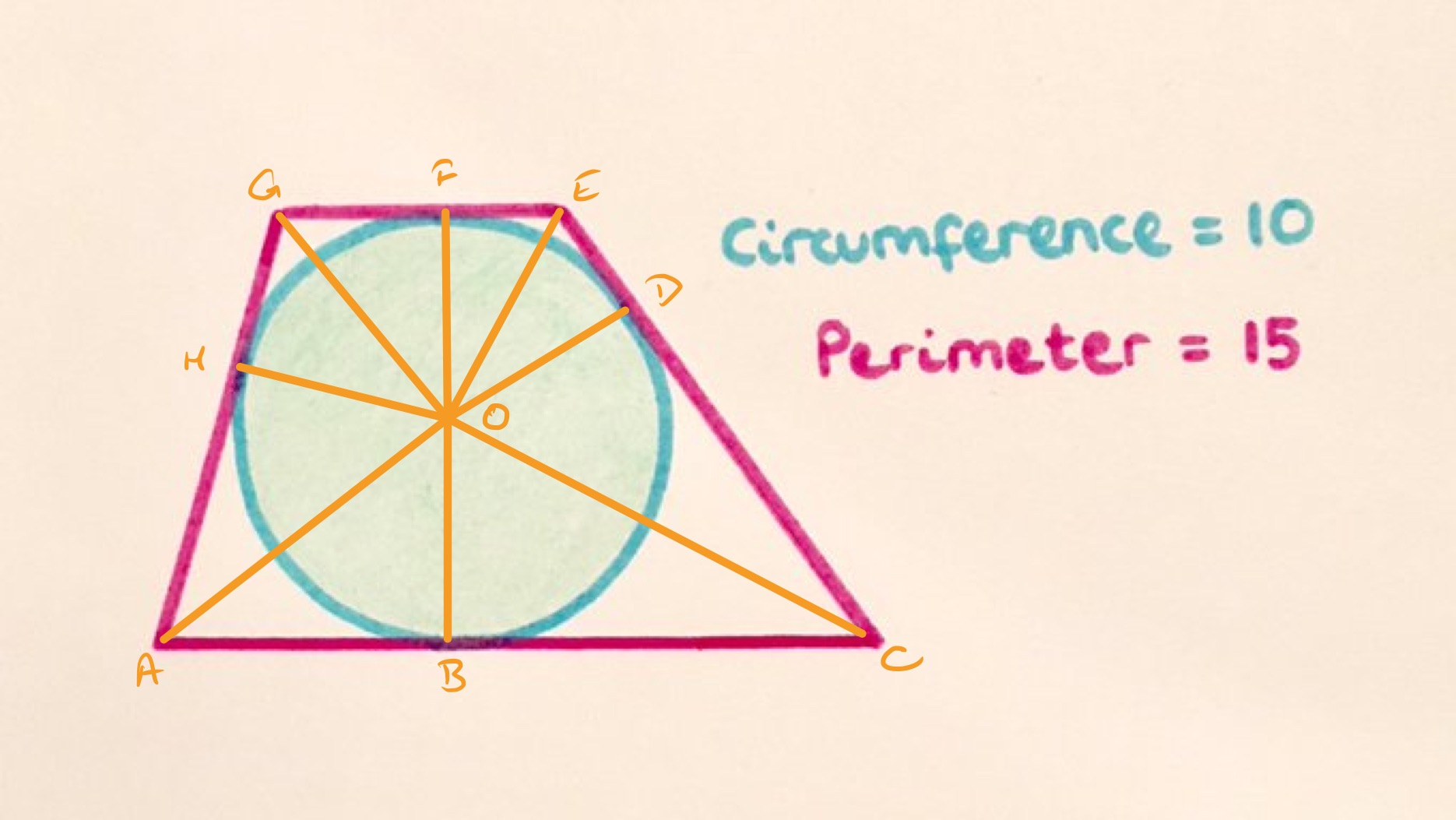
In the above diagram, the point labelled is the centre of the circle and the points , , , and are where the sides of the trapezium meet the circle.
Consider triangles and . These are both right-angled triangles since and are both the angle between a radius and tangent. They share the side as their hypotenuse, and the sides and are the same length as they are radii of the same circle. Therefore triangles and are congruent. So the lengths of and are the same. A similar argument holds at each other vertex of the trapezium. So writing , , , and for the lengths of , , , and respectively, the perimeter of the trapezium is and this is equal to .
Let be the radius of the circle, then from considering the circumference of the circle, .
The area of the trapezium is given by:
The area of the circle is given by:
The fraction of the trapezium that is shaded is therefore .