Notes
three aligned triangles solution
Three Aligned Triangles
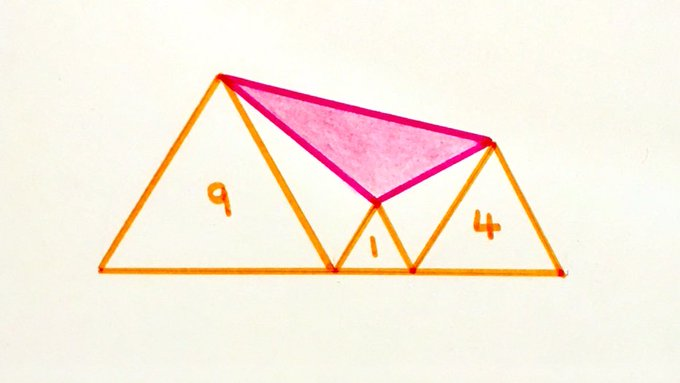
Given the areas of the three equilateral triangles, find the shaded area.
Solution by Lengths in Equilateral Triangles and Area Scale Factor
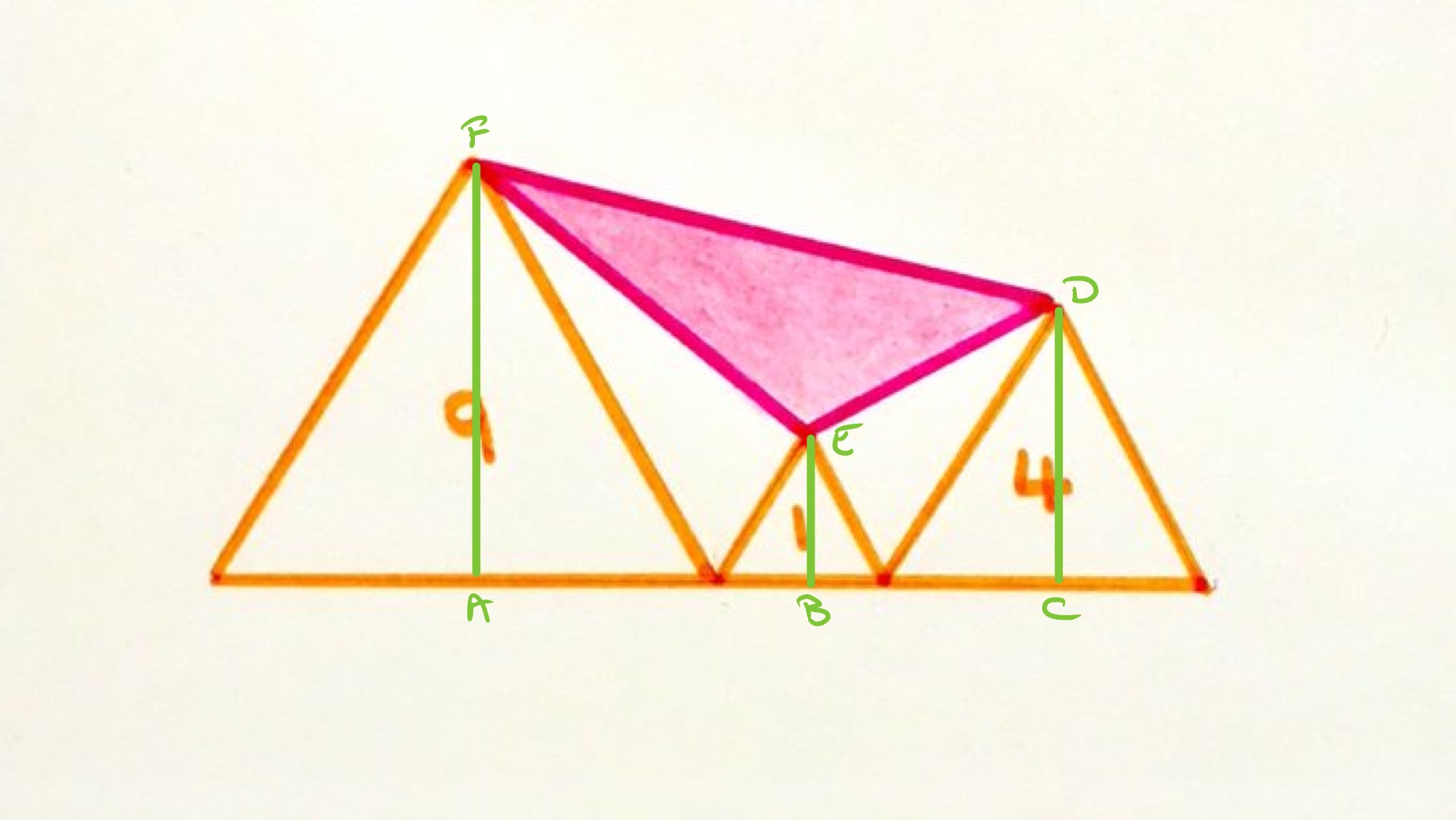
Let be half the side length of the smallest triangle. Using the relationships between lengths in an equilateral triangle, the length of is . The area scale factors to the other triangles are and , so the length scale factors are and . Therefore has length and has length , while has length and has length .
The area of the shaded triangle can be found by taking the area of trapezium and subtracting the areas of the trapezia and . This is given by:
The area of the smallest equilateral triangle is given by , so this is equal to . Hence the area of the shaded region is .