Notes
subdivided triangle solution
Subdivided Triangle
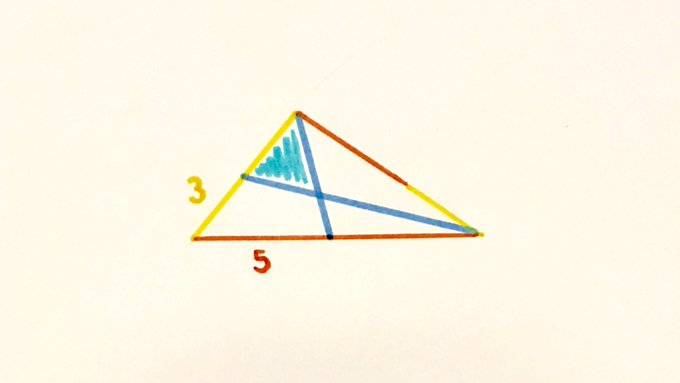
Red segments have length , and yellow segments have length . What’s the shaded area?
Solution by Pythagoras' Theorem and Crossed Trapezium
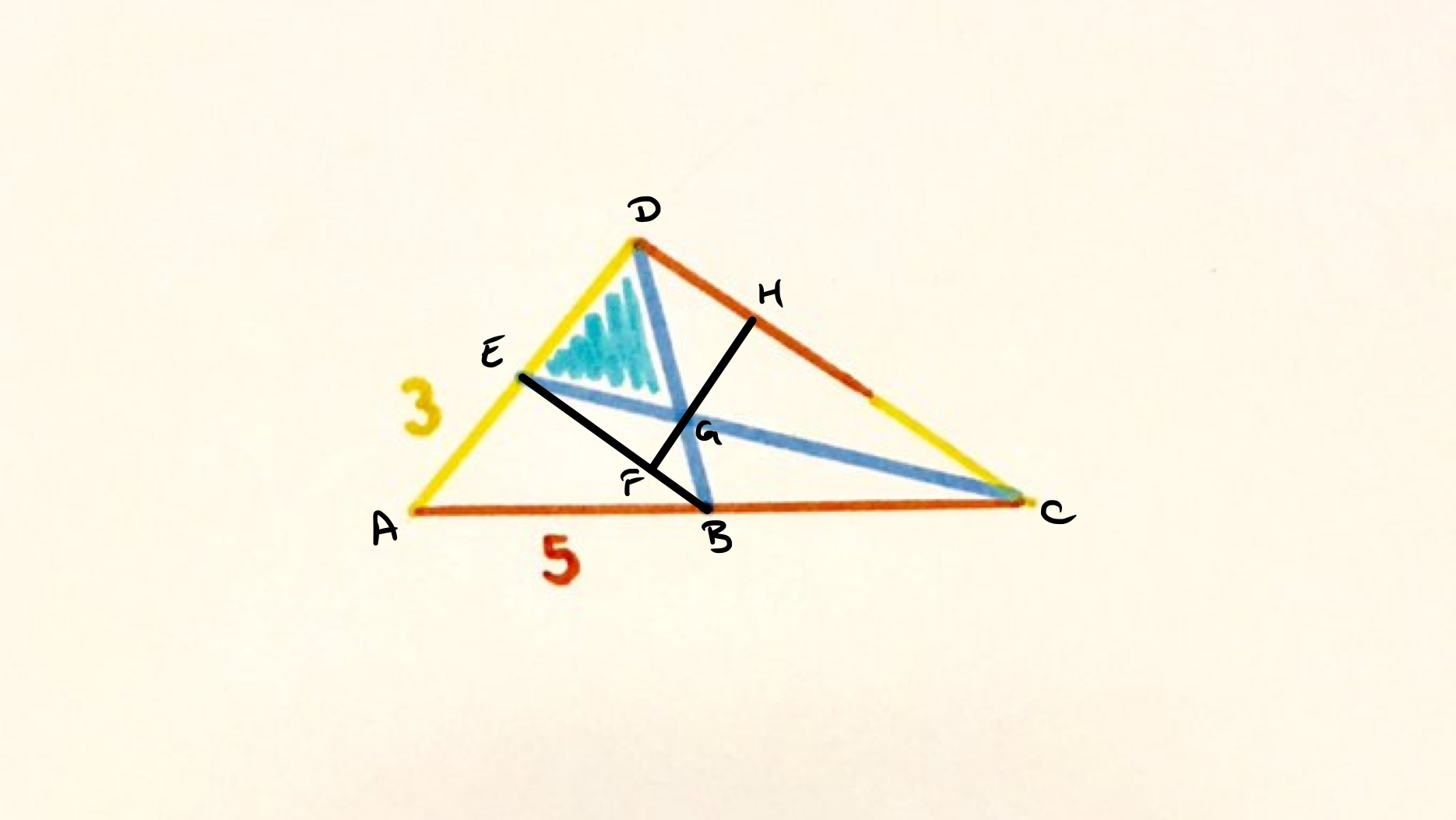
Since the yellow segments have length and the red have length , the side lengths of the triangle are , , and . These satisfy which means that triangle is right-angled by the converse to Pythagoras' Theorem.
As is the midpoint of and of , is parallel to and so is a trapezium. With the diagonals, this makes a crossed trapezium. The scale factor from to is , so the area of the trapezium is times the area of triangle . Since has length , length , and has length the area of the trapezium is so triangle has area . Then triangle has area .