Notes
quadrilateral from two squares in a square solution
Solution to the Quadrilateral from Two Squares in a Square Puzzle
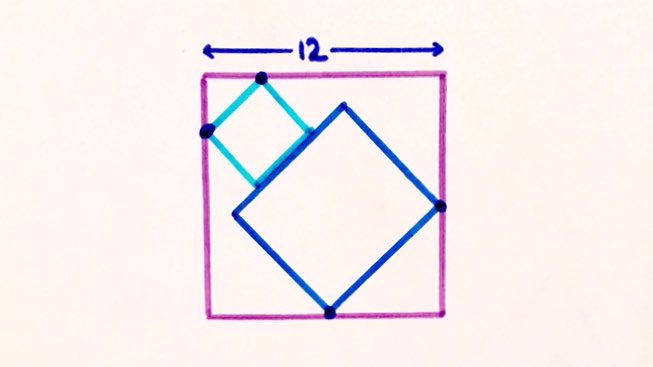
Join the four points where the inner squares touch the outer square to make a quadrilateral. What’s its area?
Solution by Area of a Trapezium and Square
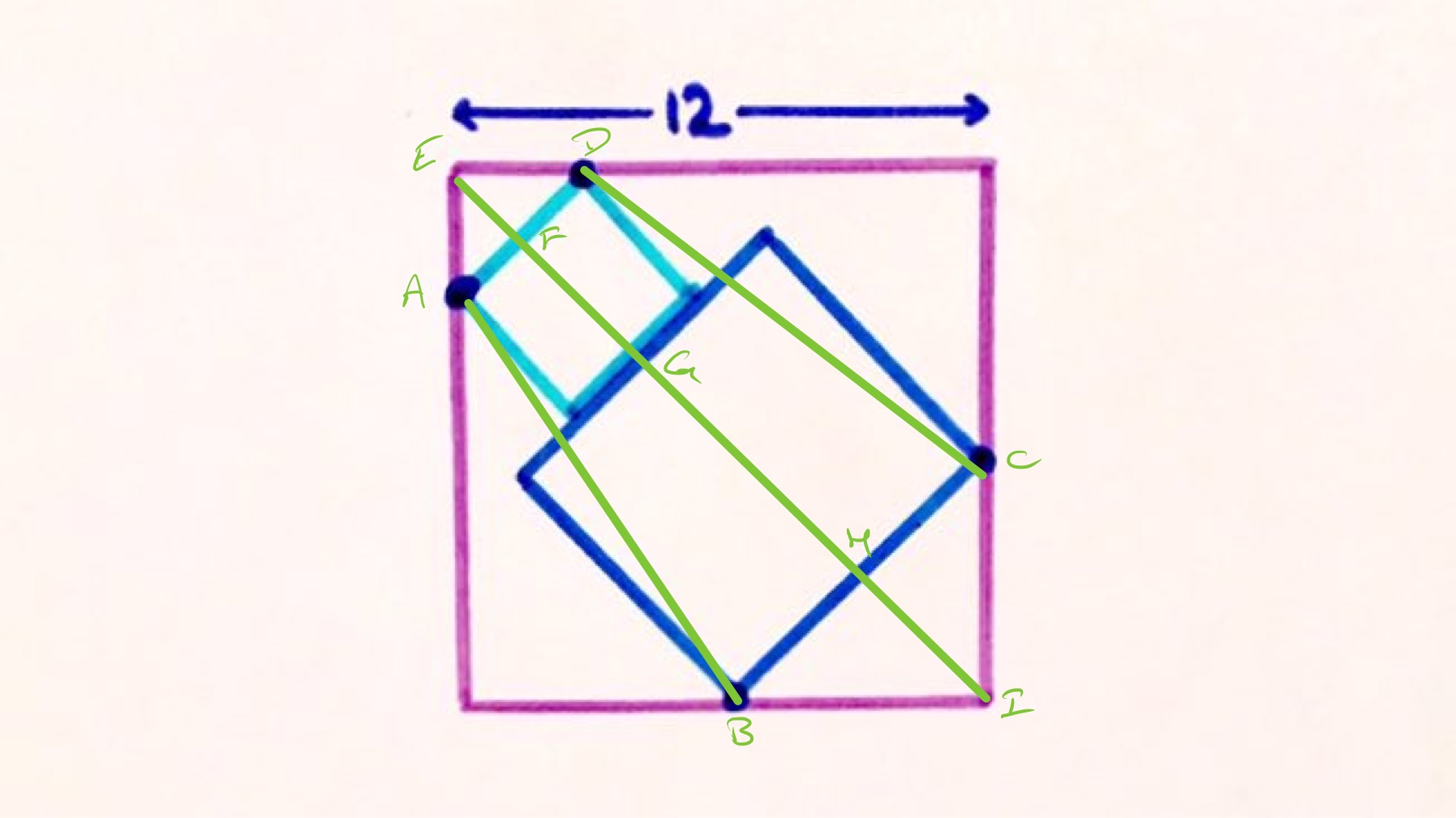
In the above diagram, the quadrilateral formed is which is a trapezium. Let be the side length of the smaller square and of the larger. The area of the trapezium is .
Consider the diagonal of the outer square. The triangle is an isosceles right-angled triangle so has the same length as , which is . Therefore has length . Similarly, has length . The diagonal then has length .
The area of a square can be calculated as half the square of the length of a diagonal, so . Rearranging this shows that .