Notes
bell-ringing braids solution
Solution to the Bell-Ringing Braids Puzzle
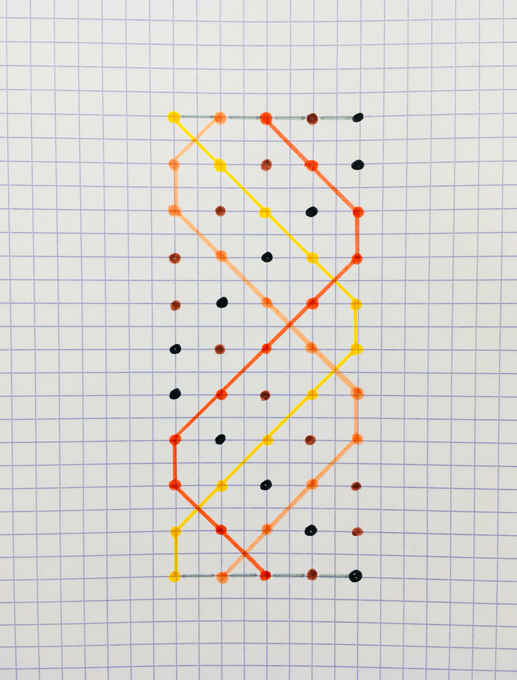
From one row to the next, each point swaps with the neighbour it didn’t swap with last time. What percentage of the grid is enclosed by the red and orange lines? By red and yellow? By other pairs of colours?
Solution by Area of a Trapezium
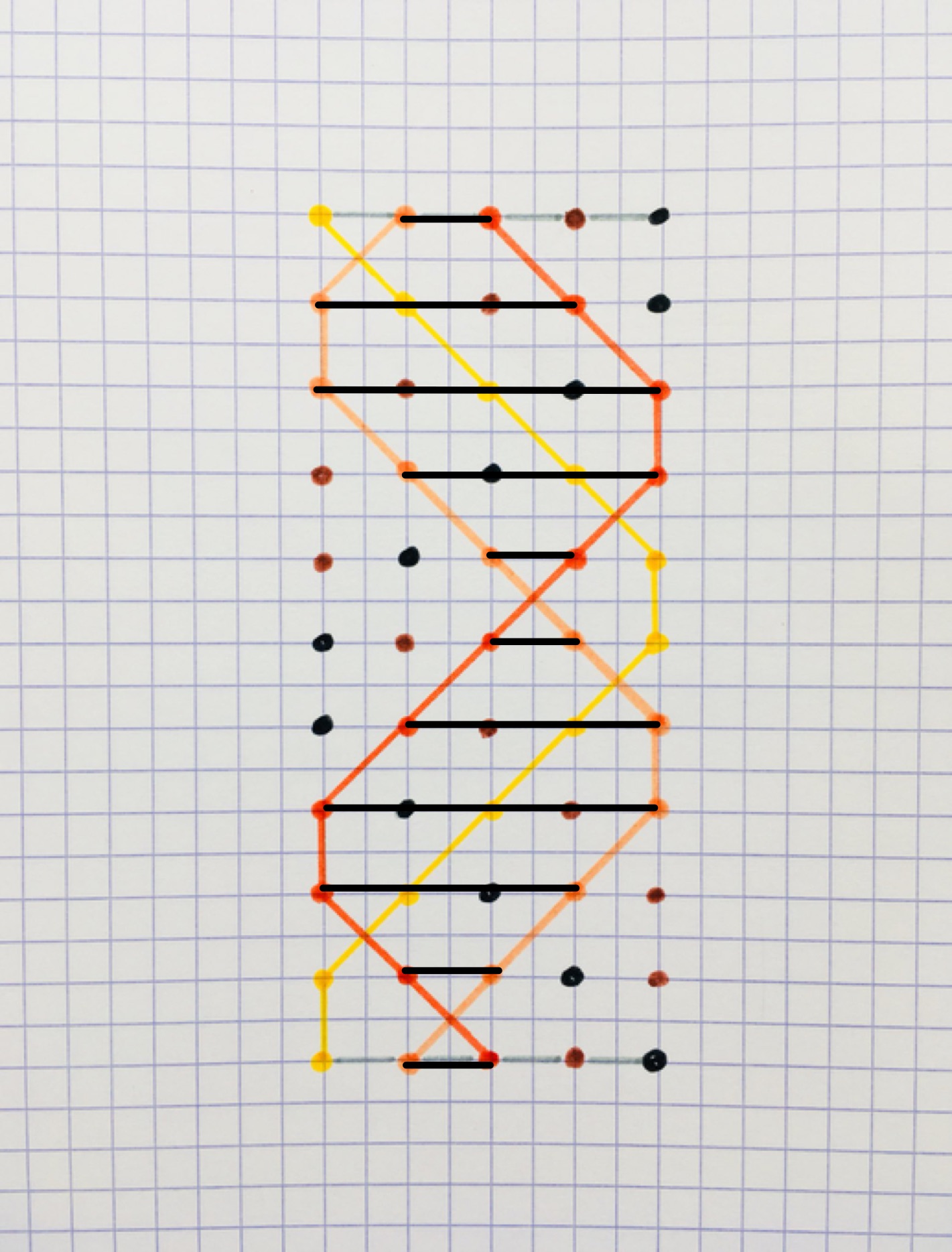
Let us use a scale wherein one unit is the side length of two small squares in the above diagram, so a square comprising four small squares has area one unit.
To work out the area enclosed by the red and orange lines, split the diagram into horizontal sections as in the above diagram. Apart from the levels where the lines cross, each section is a trapezium. The area enclosed by the red and orange lines on the first four levels is therefore:
The numbers appearing in this sum are the horizontal separations at each stage between the strands under consideration.
The next level contains a crossing. If the strands did not cross at that point then the pattern above would continue with a “trapezium” with parallel sides of lengths and (otherwise known as a “square”). The crossing means that there are two side triangles cut out of this square, which have a total area of . So if we continue the above pattern, for every crossing we have over-counted by a half. The full area is therefore:
Since the strands end up in the same positions as they start, the first and last terms in the sum can be combined to a single term.
This gives an area of . The full area of the grid is , so as a fraction of this grid this is .
For the red and yellow lines, the sum is:
All of the other possibilities are the same as one or other of these two:
- : yellow-orange, orange-brown, brown-green, green-red, red-yellow
- : yellow-brown, brown-red, red-orange, orange-green, green-yellow