Notes
divided hexagon solution
Solution to the Divided Hexagon Puzzle
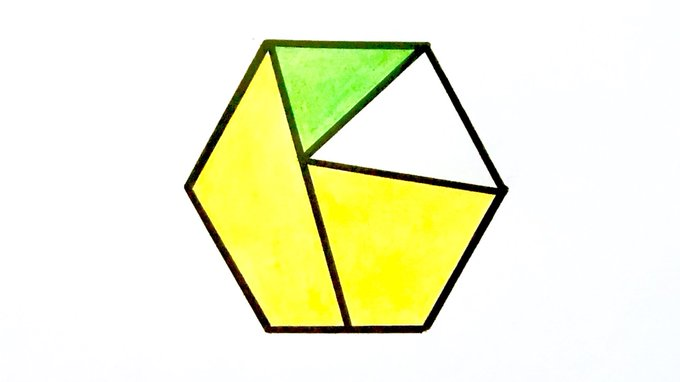
Each yellow region covers one third of the regular hexagon. What fraction is green?
Solution by Properties of a Regular Hexagon, Area of a Trapezium, and Area of a Triangle
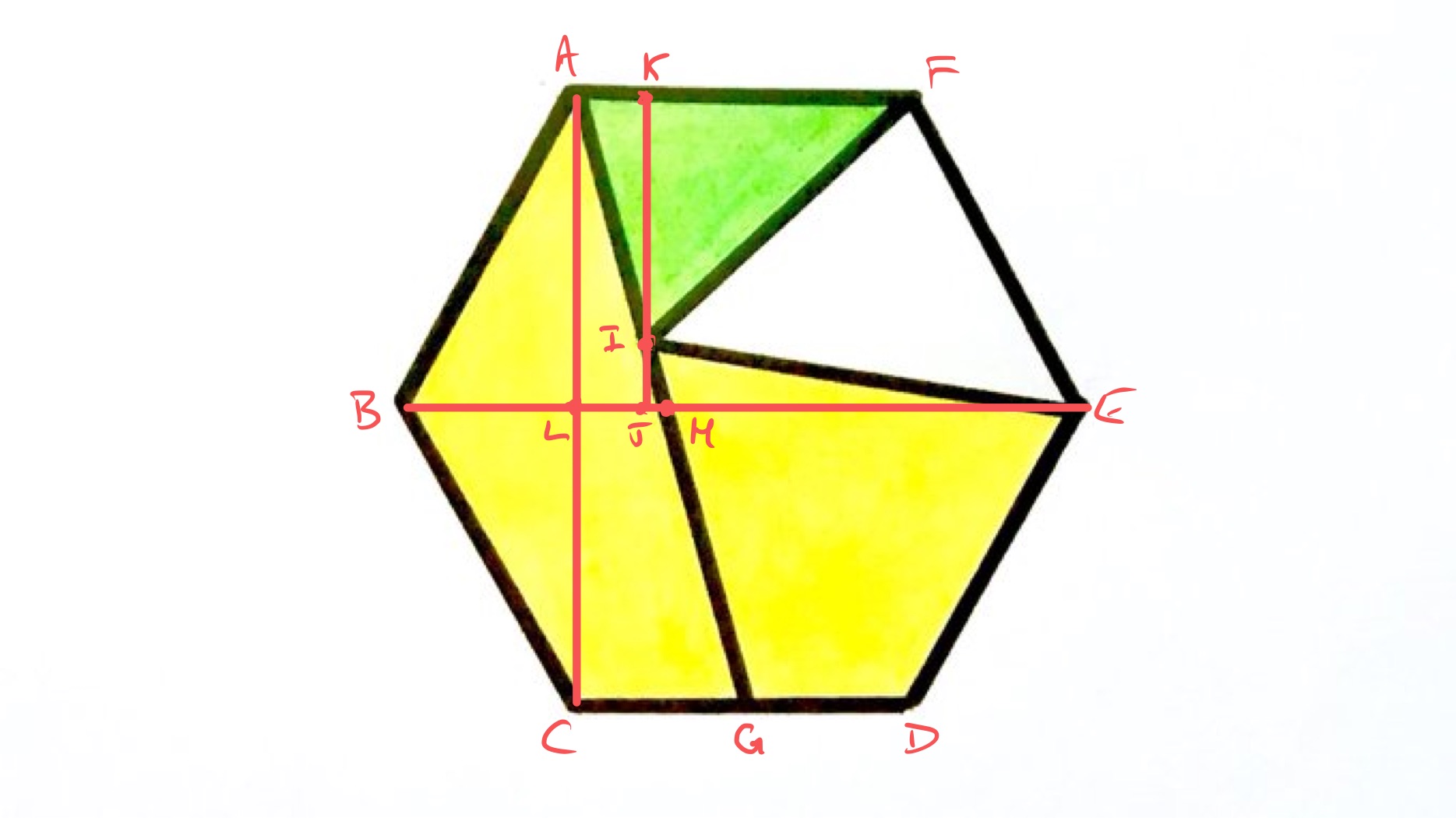
Consider the points labelled as above. Let be the side length of the hexagon, and let be the half-height, so has length . The area of the hexagon is then .
The length of is so triangle has area which is one sixth of the area of the hexagon, so triangle also has area . As its height is , the length of must be and so is the midpoint of .
Then as is half way along , has length (since has length ). Therefore has length , so trapezium has area . This is ths of the area of the hexagon, so the area of triangle is . Since has length , this means that (the height of above ) has length . So has length and the area of the green triangle is .
This is ths of the area of the hexagon.