Notes
semi-circle on a hexagon solution
Solution to the Semi-Circle on a Hexagon Puzzle
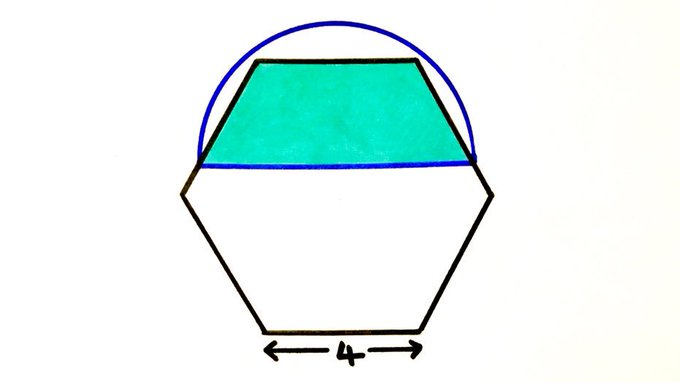
One third of this regular hexagon is shaded. What’s the area of the semicircle?
Solution by Area of a Trapezium and Semi-circle, Similarity, and Properties of a Regular Hexagon
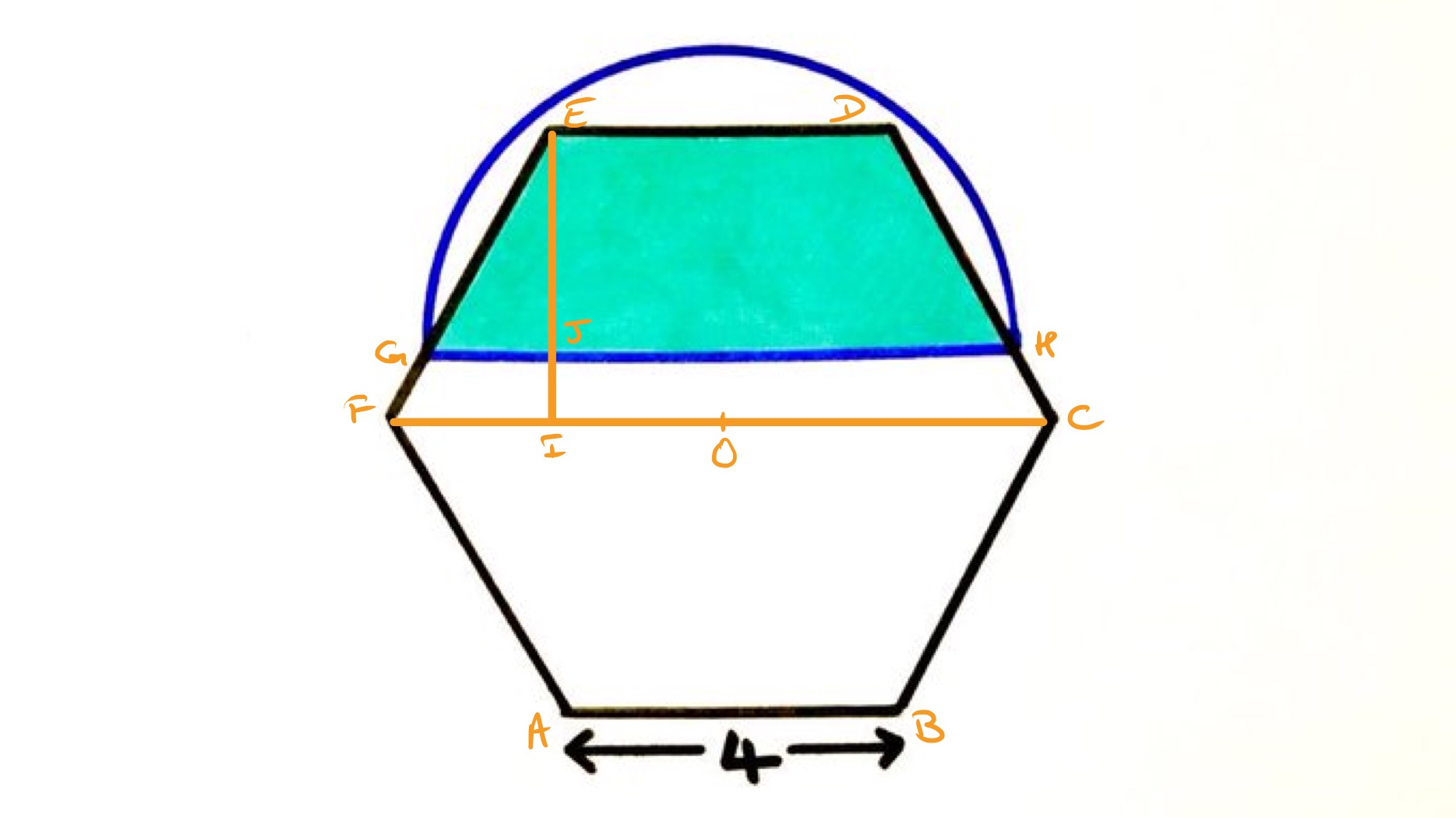
In the above diagram, the point labelled lies on below so that angle is a right-angle. Since is the midpoint of , which has length , has length .
Let be the length of , so has length , and let be the length of . Then as triangles and are similar, has length . From the formula for the area of a trapezium, the shaded region has area
Since is the height of one of the six equilateral triangles making up the hexagon, the area of the is . So since the shaded area is one third of the hexagon:
which simplifies to .
The radius of the semi-circle is so its area is
From above, , so the area simplifies to: