Notes
overlapping hexagons solution
Solution to the Overlapping Hexagons Puzzle
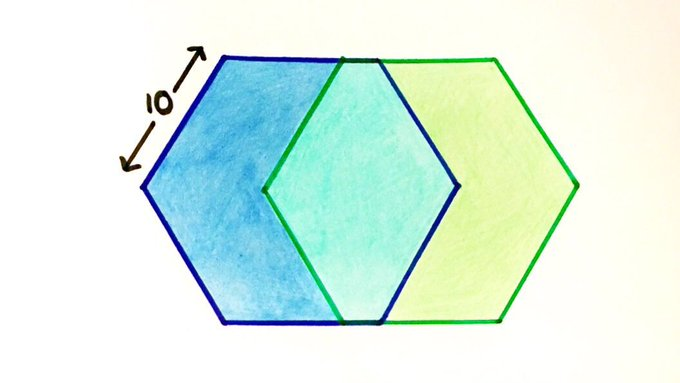
Two regular hexagons overlap to create three equal areas. What’s the perimeter of the design?
Solution by Areas of Trapezium and Parallelogram
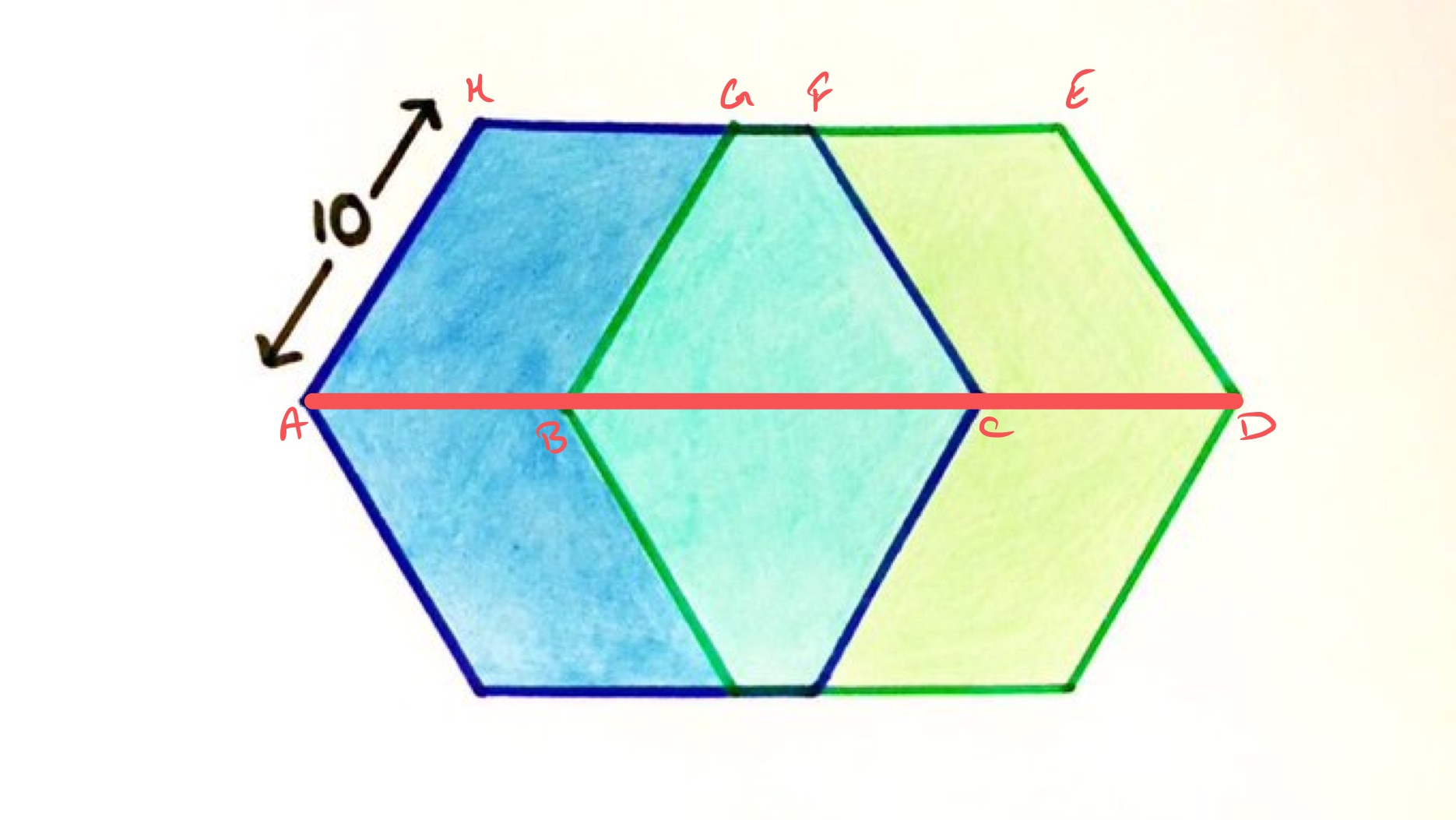
Consider the parallelogram and the trapezium . As the hexagons are regular, has length and has length . Let be the length of . Then has length and has length . Let be the perpendicular distance between and . The parallelogram then has area and the trapezium has area . As these have the same area, so .
The length of is then , so the perimeter of the design is .