Notes
inverse star in a rectangle solution

Solution to the Inverse Star in a Rectangle Puzzle

Solution by Properties of an Equilateral Triangle

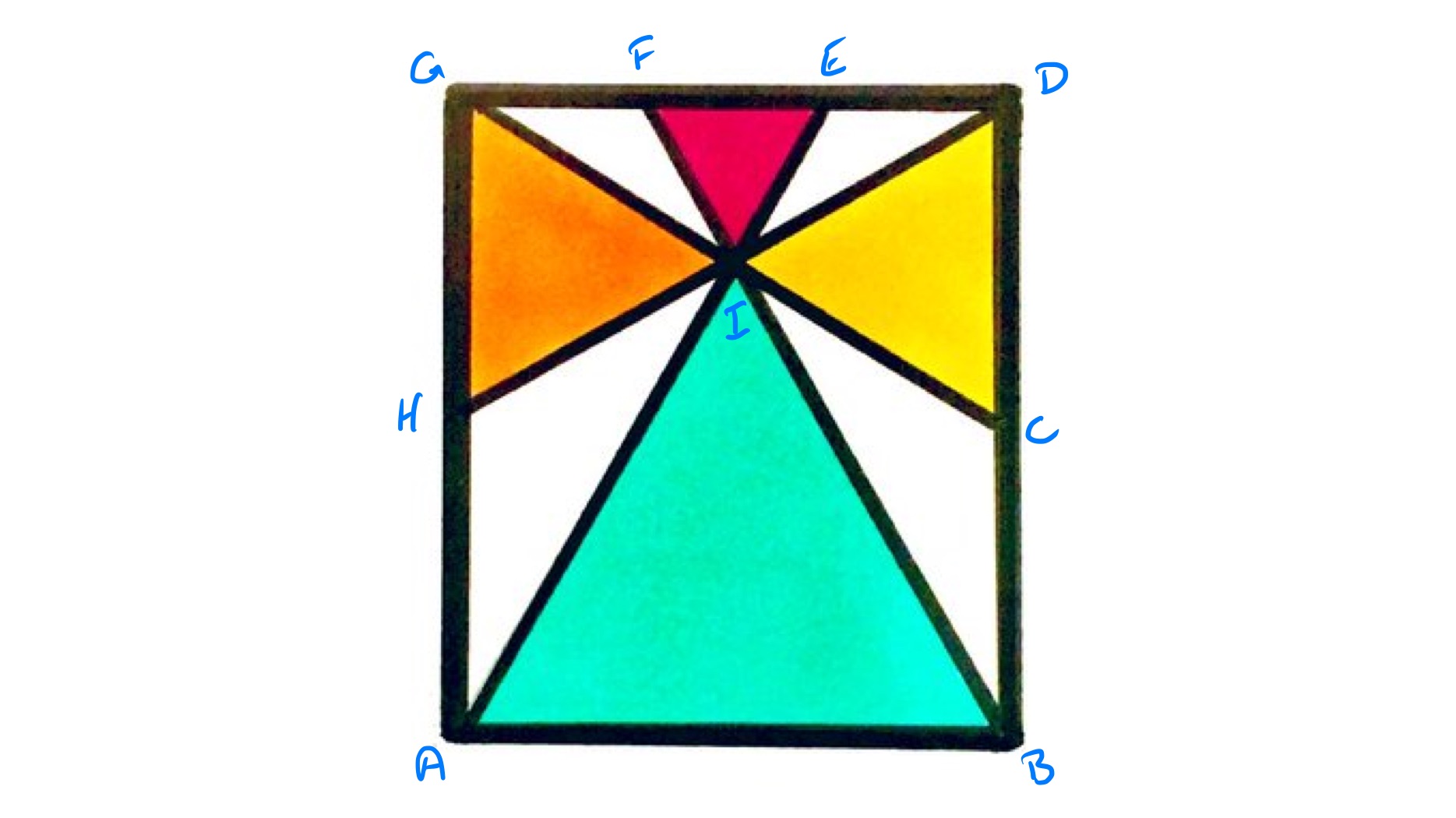
In the above diagram, let $x$ be the length of the side $A B$. The “height” of the yellow triangle, which is the perpendicular distance of $I$ to the side $D C$ is half that, so from lengths in an equilateral triangle, the length of $D C$ is $\frac{x}{\sqrt{3}}$. The height of $I$ above $A B$ is $\frac{x \sqrt{3}}{2}$ so the full height of the rectangle is:

The area of the rectangle is therefore $\frac{2 x^2}{\sqrt{3}}$.

The height of the red triangle, being the perpendicular distance of $I$ to $F E$, is half the length of $D C$ meaning that $F E$ has length $\frac{x}{\sqrt{3}} \div \sqrt{3} = \frac{x}{3}$. The area of an equilateral triangle is $\frac{\sqrt{3}}{4}$ times the square of its side length, so the total area of the triangles is:

This means that the equilateral triangles cover $\frac{2}{3}$rds of the rectangle.

Solution by Isosceles Triangles

With the points labelled as in the above diagram, triangle $I C B$ is isosceles because angle $I \hat{C} B$ is $120^\circ$ and angle $C \hat{B} I$ is $30^\circ$. This means that $I C$ is the same length as $C B$, so triangle $I D C$ has the same “base” length as $I C B$ (along $D B$) and they both have $I$ as apex above this length, hence they have the same area. By the same argument, triangles $I E F$ and $I D E$ have the same area.

The four triangles therefore have the same area as the trapezium $A E D B$. Moreover, $E D$ is a third of the length of $G D$. Comparing the trapezium area with the rectangle shows that the trapezium is $\frac{2}{3}$rds of the area of the rectangle.