Notes
three regular hexagons iii solution
Solution to the Three Regular Hexagons iii Puzzle
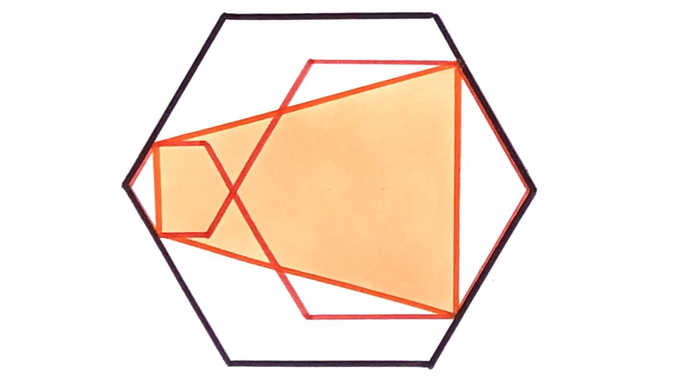
Three regular hexagons. What fraction of the large hexagon is shaded?
Solution by Lengths in a Regular Hexagon and Area of a Trapezium
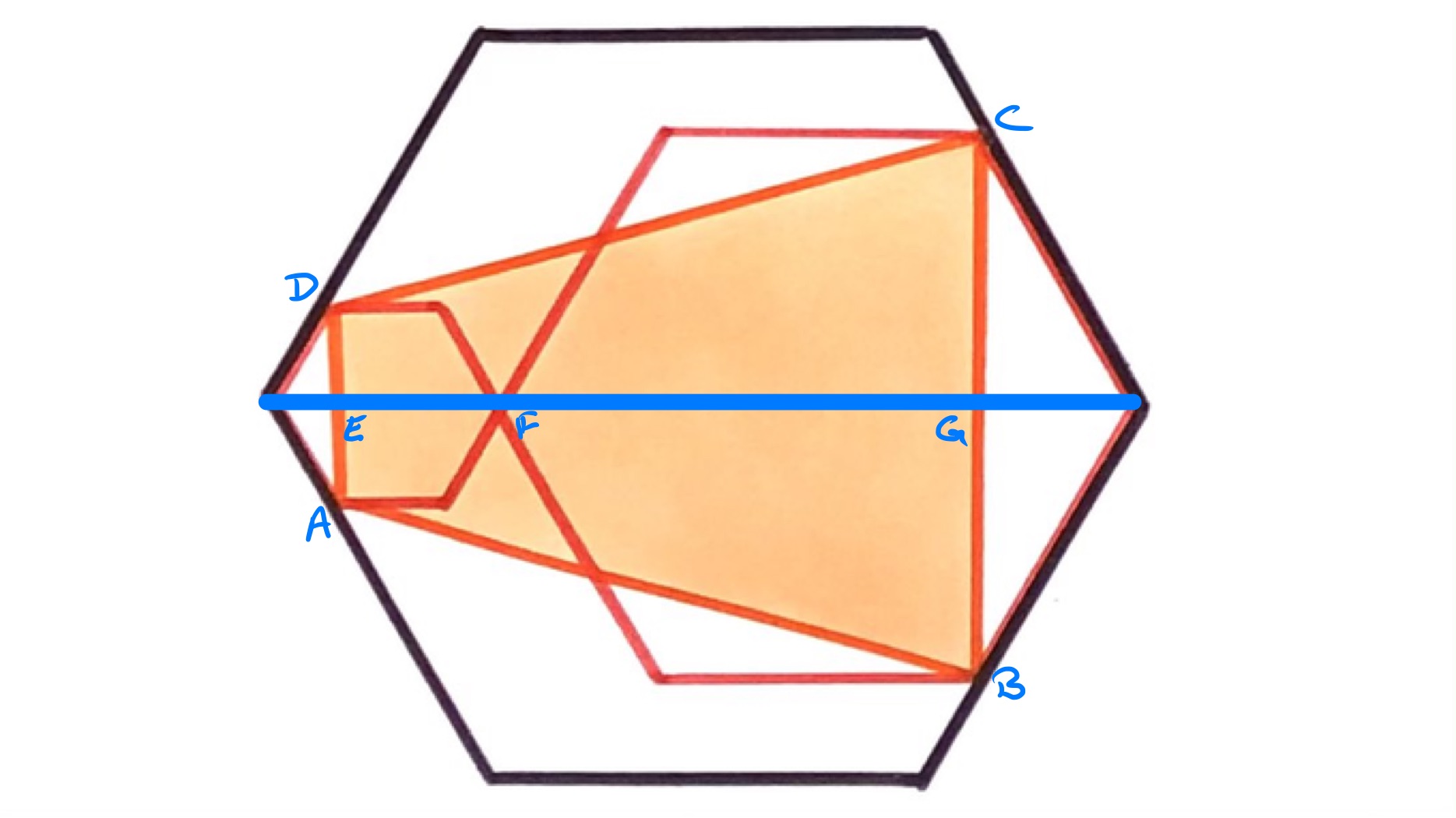
Let , , and be the side lengths of the three hexagons in increasing order. Then as the largest diameter in a regular hexagon is twice its side length, by considering the largest diameter of the larger hexagon then . Using the relationships between lengths in a regular hexagon, has length while has length . The length of is and of is . So the length of is . Using the formula for the area of a trapezium, the area of is:
This simplifies to .
The area of the outer hexagon is . Therefore, the shaded area is half the area of the outer hexagon.
Solution by Invariance Principle
There are two configurations of the hexagons that make the solution clear.
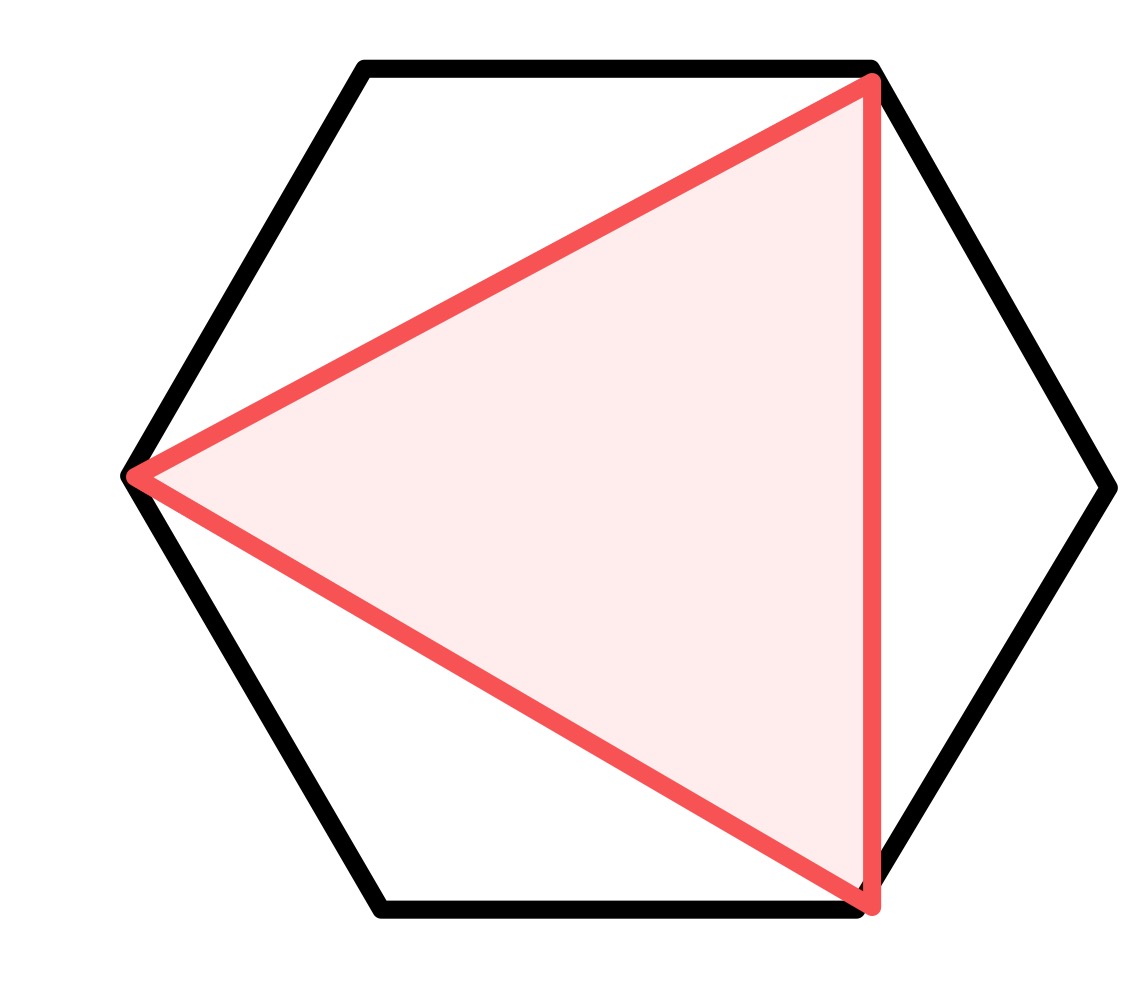
In this one, the left-hand hexagon has zero size, whereupon the other two hexagons are of equal size and the shaded area is an equilateral triangle inside the hexagon, so has half the area of the hexagon.
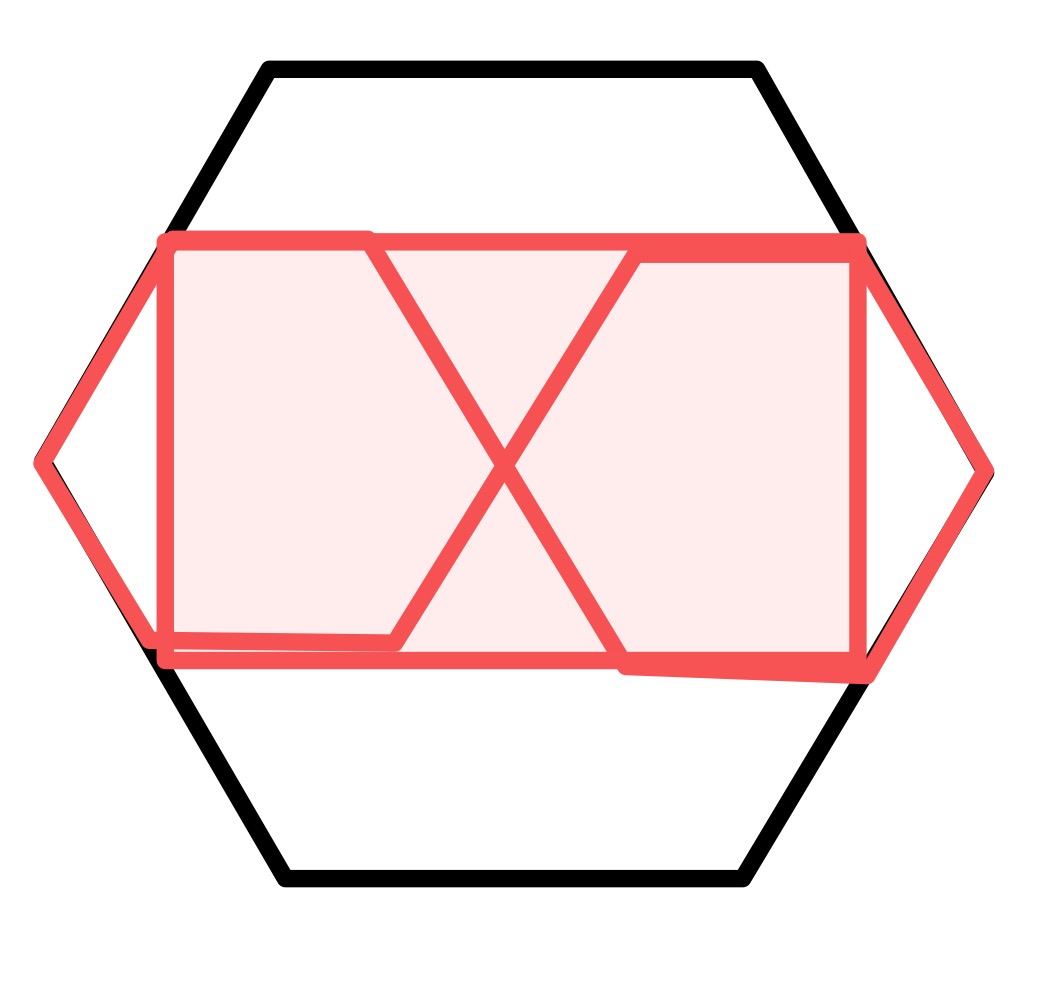
In the second, the hexagons are of equal size making the shaded region a rectangle. A decomposition argument shows that the area of the rectangle is the same as that of the two hexagons combined. Each hexagon is half the size, in length, of the outer hexagon meaning each has a quarter of the area so combined they cover half the area of the outer hexagon.