Notes
overlapping squares solution
Solution to the Overlapping Squares Puzzle
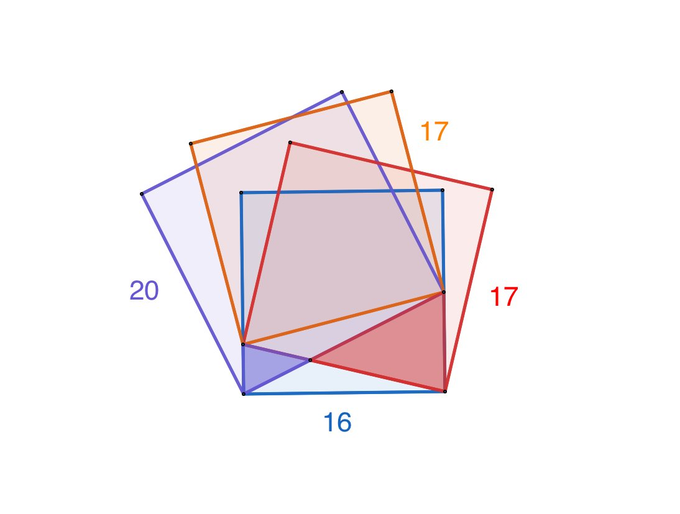
The numbers show the areas of the overlapping squares. What’s the difference between the areas of the red and purple triangles?
Solution by Pythagoras' Theorem, Area of a Square, and Crossed Trapezium
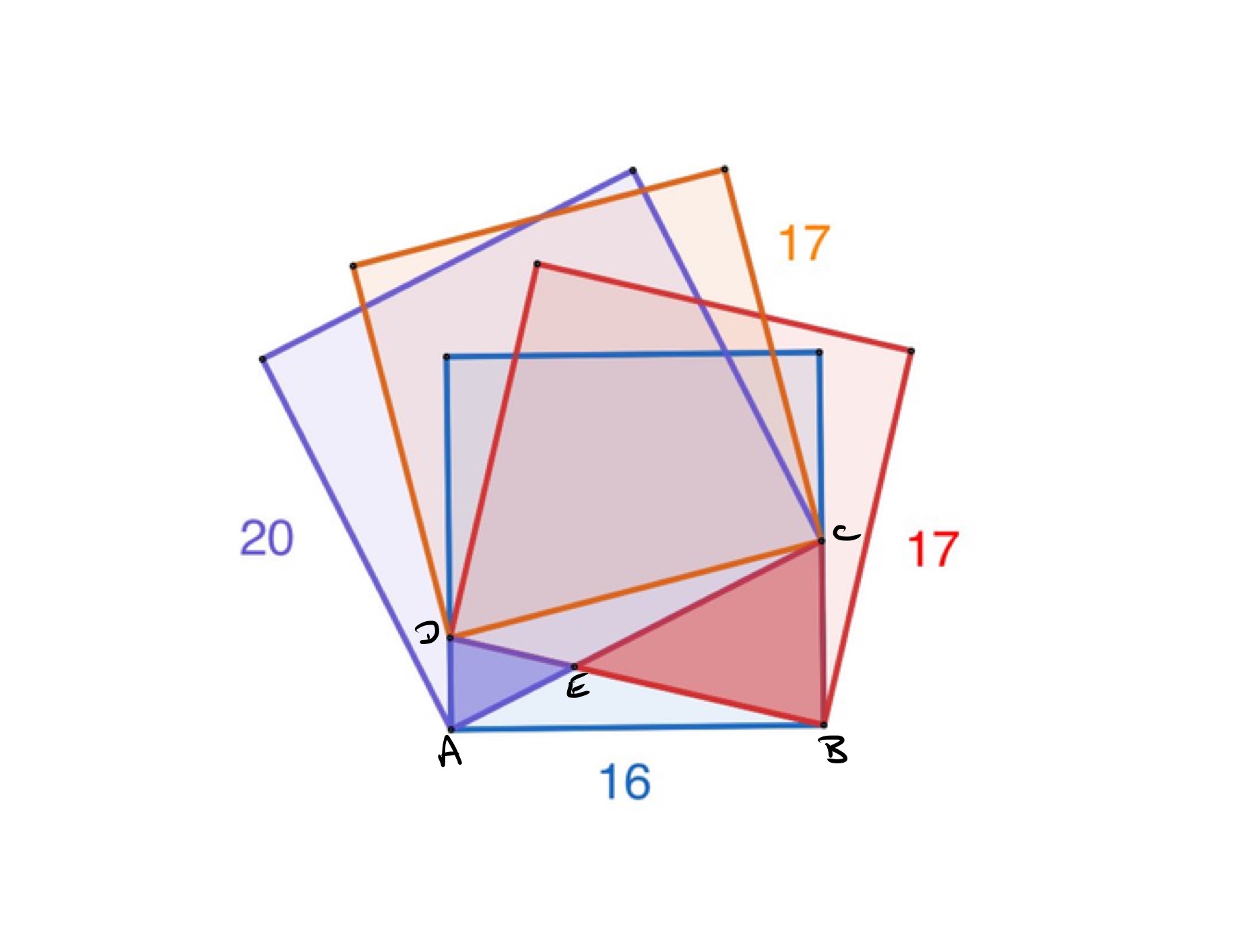
With the points labelled as in the above diagram, let be the length of , of , of , of , and of . As several of these are sides of squares, then , , and . In particular, .
Triangle has a right-angle at , so Pythagoras' theorem applies and shows that which rearranges to , so . A similar argument applied to triangle shows that so .
Triangles and are part of a crossed trapezium and so are similar. The length of is twice that of , so the height of above is twice that of above . Since these heights must add up to the length of , which is , then is above and above . The areas of the triangles are therefore and respectively. Their difference is therefore .