Notes
crossed hexagon solution
Crossed Hexagon
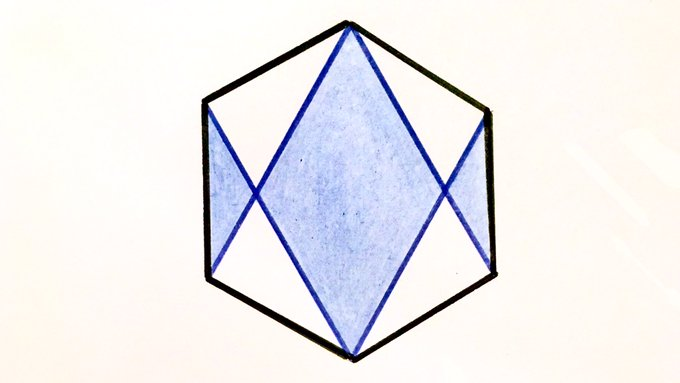
What fraction of the regular hexagon is shaded?
Solution by Similar Triangles and Vertically Opposite Angles
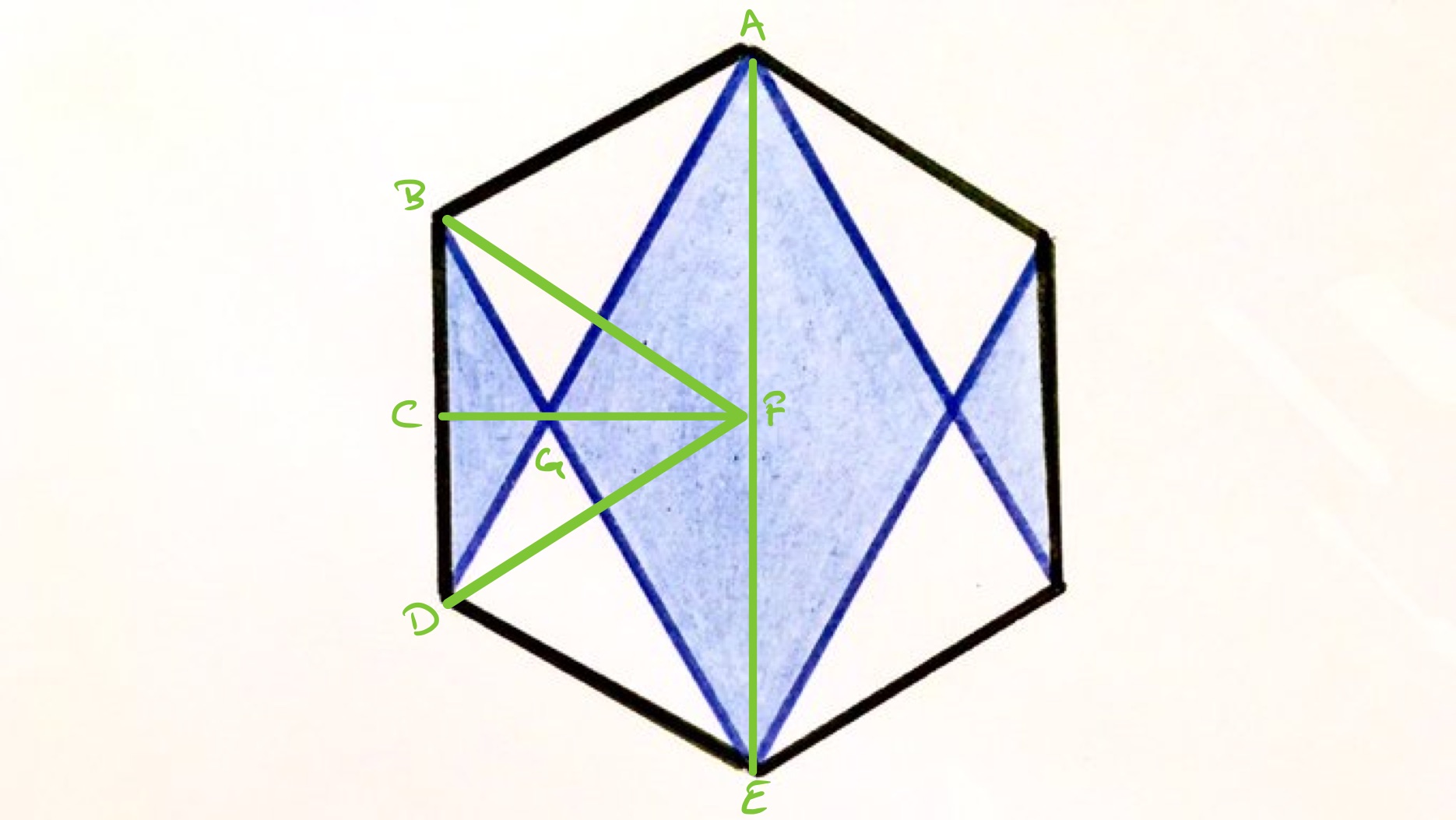
In triangles and , the sides and are parallel, and the angles and are vertically opposite and so equal. Therefore, triangles and are similar. Since has twice the length of , the length scale factor is and the area scale factor is . The length of is twice that of , so has length one third of that of . Triangle is an equilateral triangle with area one sixth of the area of the whole hexagon. So the area of is th of the area of the whole hexagon. Triangle then has area four times that, so has area ths of the whole hexagon. Therefore, the area of the shaded region is ths of the hexagon.
Solution by Crossed Trapezium
The quadrilateral with its diagonal lines is a crossed trapezium. In such, the areas of the four triangles are in the ratio where is the ratio of the parallel sides. Therefore the ratio of the area of the shaded region to the whole trapezium is . As , this is . Since the other half is a copy of this trapezium, that ratio then holds for the whole hexagon.