Notes
equilateral triangle in a hexagon solution
Solution to the Equilateral Triangle in a Hexagon Puzzle
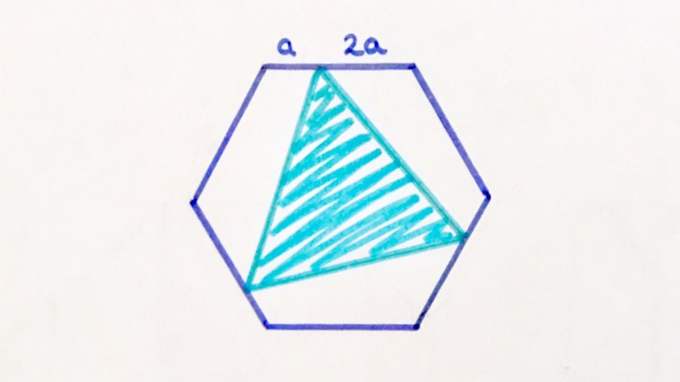
What proportion of the hexagon is shaded?
Solution by Properties of a Regular Hexagon, Area of a Trapezium, and Area of a Triangle
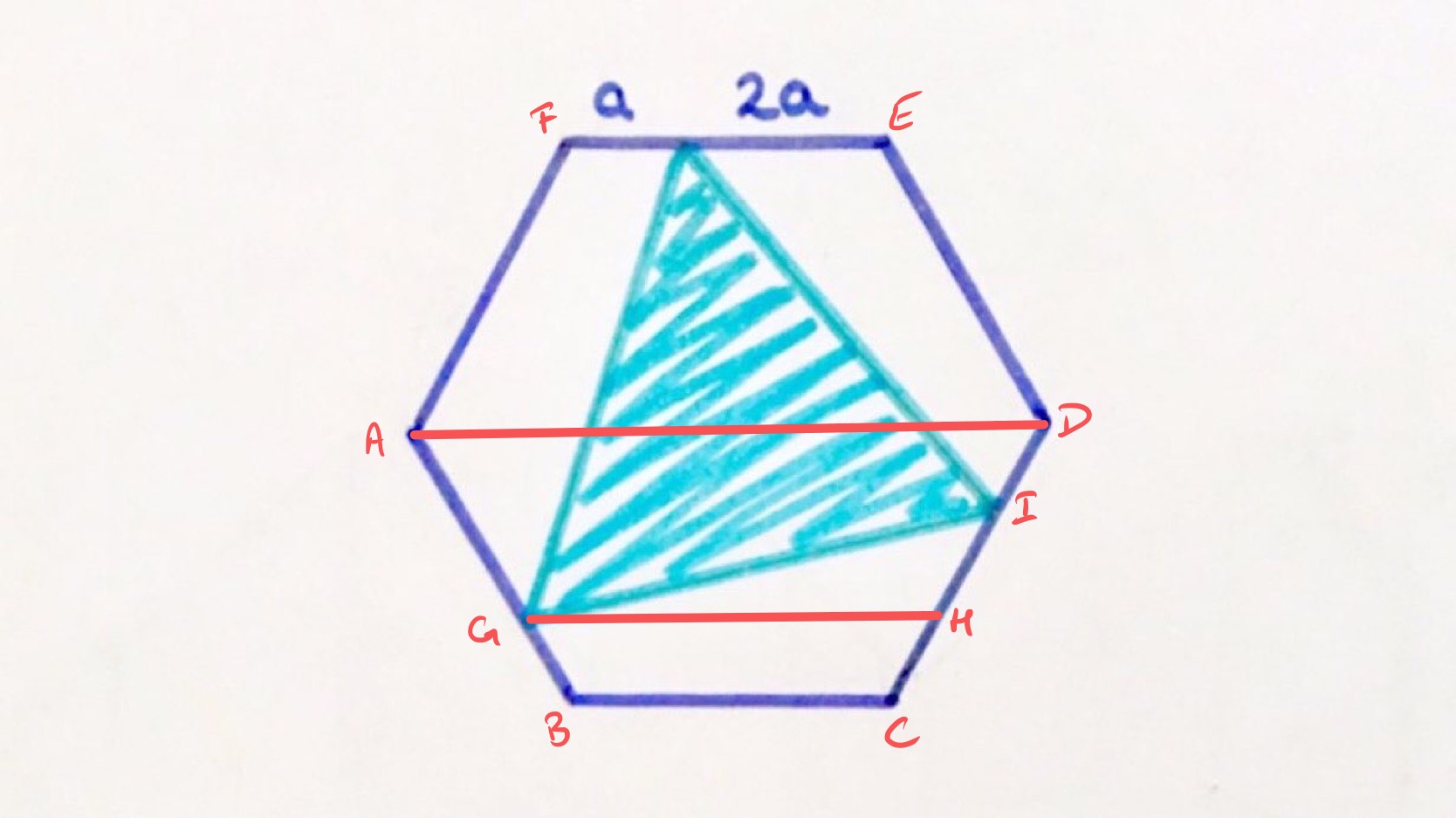
With the points labelled as above, let be half the height of the hexagon. The side length is , so the area of the hexagon is .
Consider the region . By symmetry, is one third of the way between and , so the distance between the lines and is . Similarly, is one third of the way from to , so the height of above is also . Since has length and has length , the length of is . So the area of is:
There are three such regions, meaning that the total unshaded area is which means that the shaded region has area and this is ths of the hexagon.