Notes
circle in pentagon in semi-circle solution

Solution to the Circle In Pentagon in Semi-Circle Puzzle

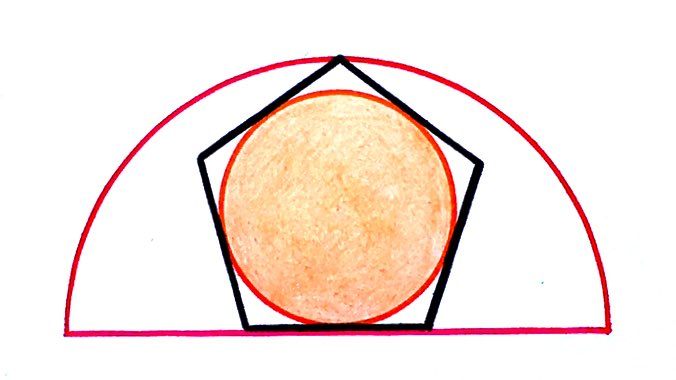
Circle In Pentagon in Semi-Circle

A circle in a regular pentagon in a semicircle. What fraction of the semicircle is shaded?

Solution by Lengths in a Regular Pentagon

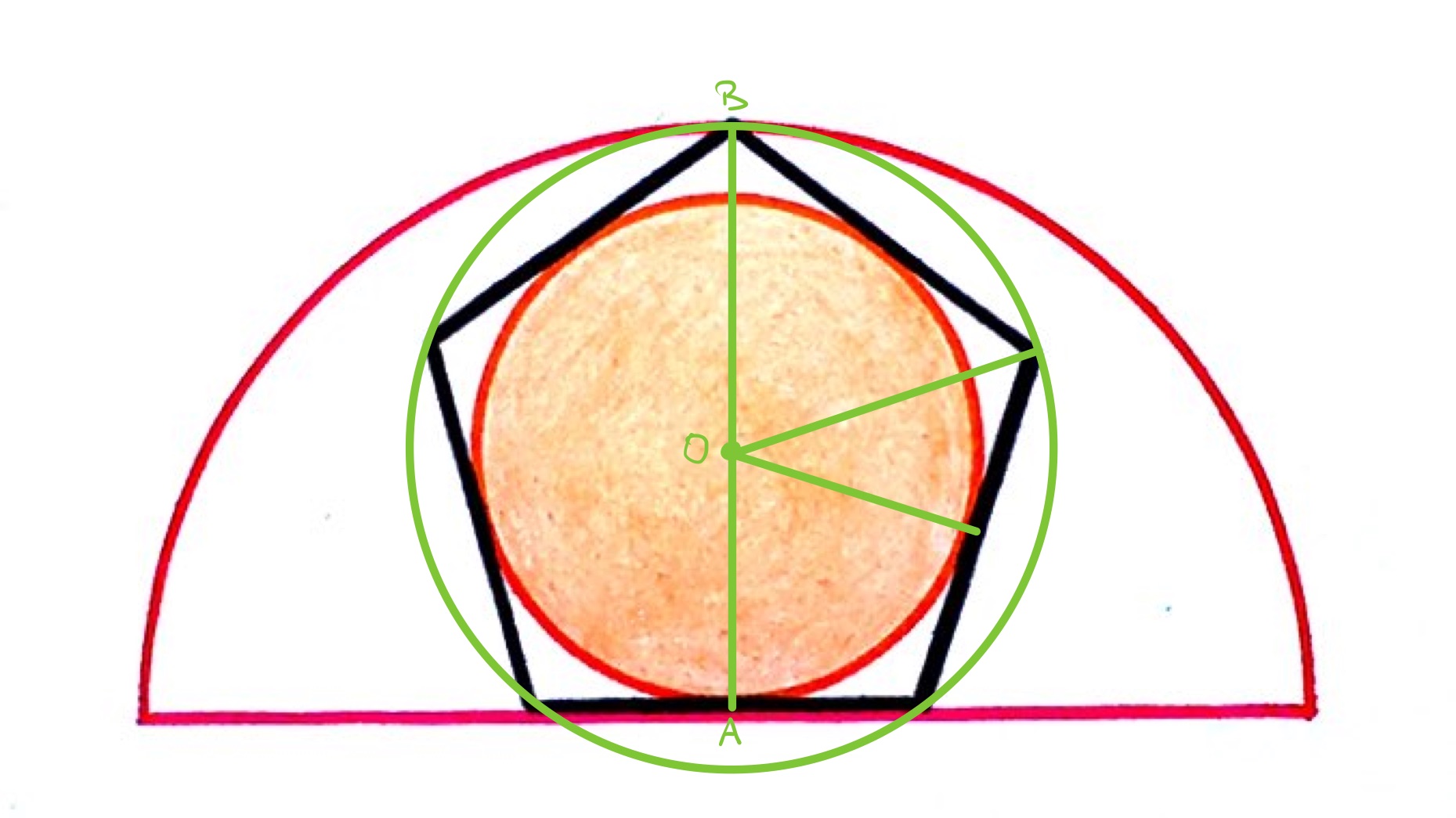
Circle in a pentagon in a semi-circle labelled

The radius of the small circle is the radius of the incircle of the regular pentagon. The radius of the semi-circle is the radius of the incircle added to the radius of the circumcircle of the regular pentagon. From lengths in a regular pentagon, these radius of the circumcircle, $R$ , and incircle, $r$ , are related by $2 r = \phi R$ where $\phi$ is the golden ratio. With this notation, the radius of the semi-circle is $r + R = (1 + \frac{2}{\phi}) r$ . The area of the incircle is $\pi r^2$ and the area of the semi-circle is:

\begin{aligned} \frac{1}{2} \pi (r + R)^2 &= \frac{1}{2} \pi (1 + \frac{2}{\phi})^2 r^2 \\ &= \frac{1}{2 \phi^2} \pi (\phi + 2)^2 r^2 \\ &=\frac{1}{2 \phi^2} \pi r^2 (\phi^2 + 4 \phi + 4) \\ &=\frac{1}{2 \phi^2} \pi r^2 5 \phi^2 \\ &= \frac{5}{2} \pi r^2 \end{aligned}

Therefore the fraction of the semi-circle that is shaded is $\frac{2}{5}$ .

Revised on February 22, 2022 20:14:29 by Andrew Stacey

Notes circle in pentagon in semi-circle solution

Solution to the Circle In Pentagon in Semi-Circle Puzzle

Solution by Lengths in a Regular Pentagon

Notes
circle in pentagon in semi-circle solution