Notes
six squares in a hexagon solution
Solution to the Six Squares in a Hexagon Puzzle
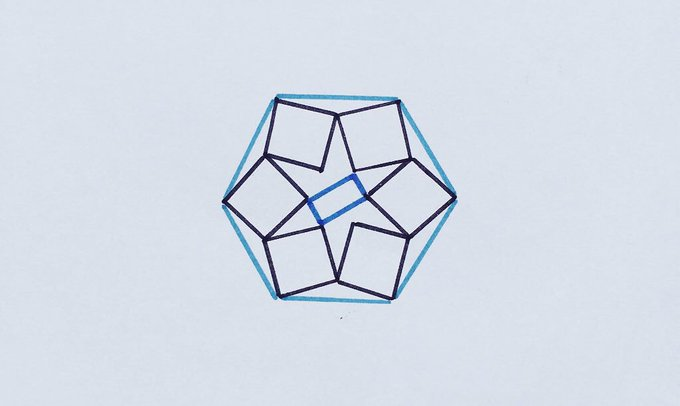
Six identical squares and a smaller rectangle are fitted into this regular hexagon. What fraction of the hexagon do they cover?
Solution by Properties of a Regular Hexagon, Isosceles Triangles, and Equilateral Triangles
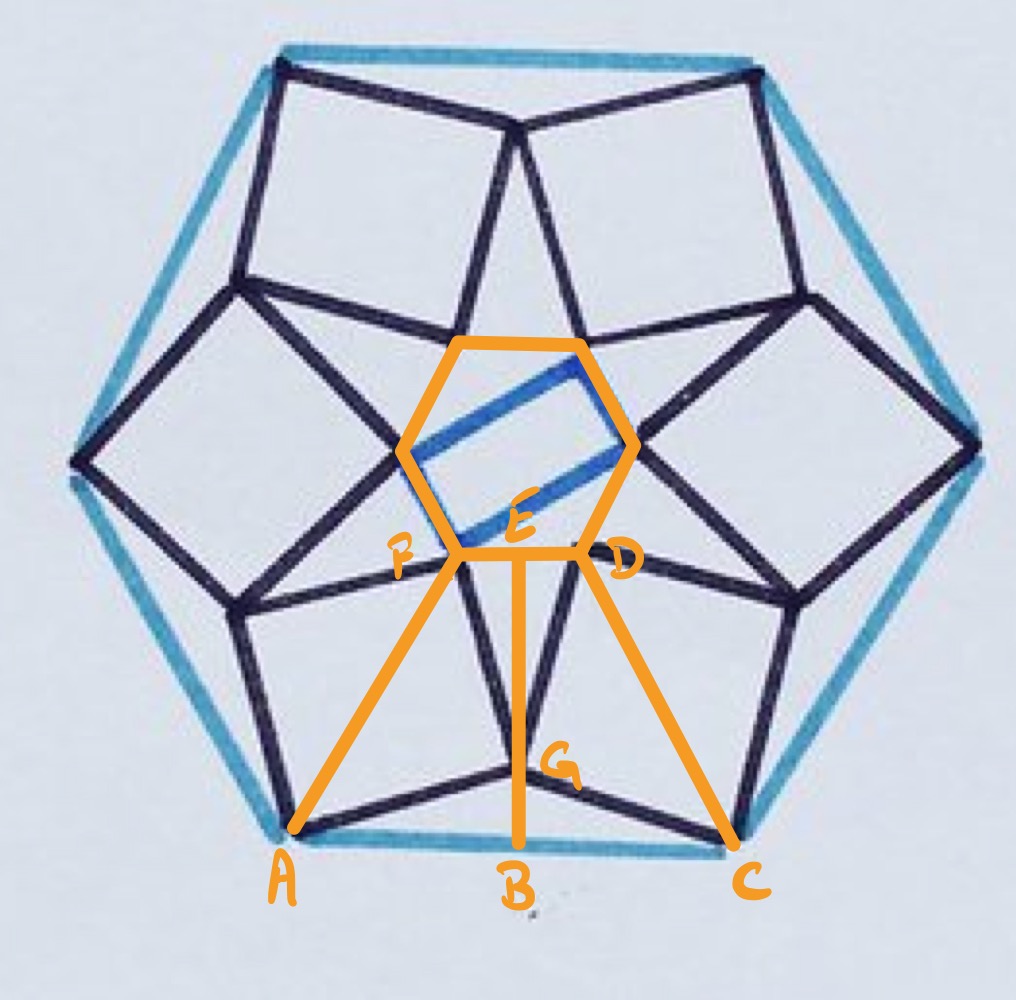
Consider the diagram labelled as above.
Using the decomposition of a hexagon into triangles, the rectangle in the inner hexagon can be seen to be of that inner hexagon.
The trapezium is divided into the half square and the two right-angled triangles and . The interior angle of a regular hexagon is , so angle is . Then angle is and so angle is also . Therefore triangles and are congruent.
To find their area, consider the isosceles triangle . This has apex angle . Placing two such triangles next to each other, as in the diagram below, we can see that the perpendicular height of above is half the length of . The area of triangle is therefore half that of .
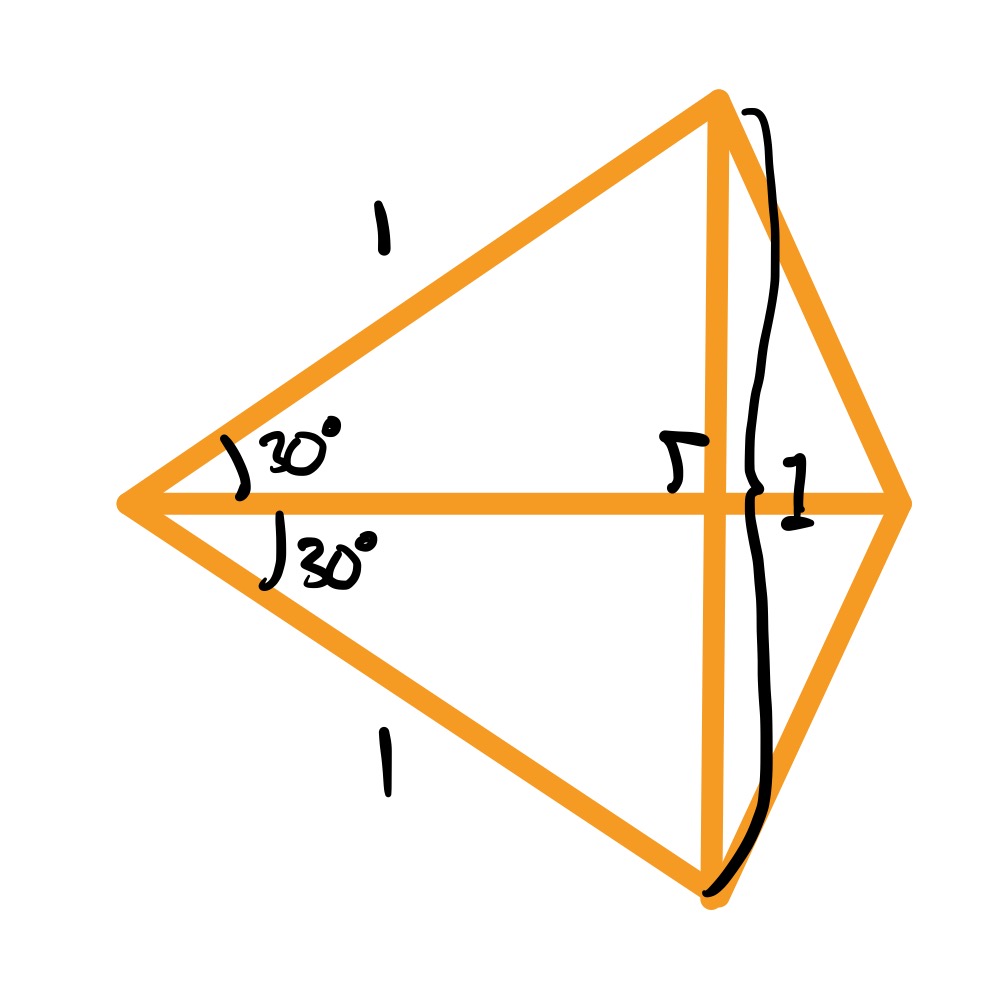
This means that the combined area of triangles and is of the area of trapezium . Equivalently, the area of triangle is of that trapezium.
So the six squares comprise of the outer ring in the hexagon, meaning that the six squares and the rectangle together make up of the area of the entire hexagon.