Notes
two regular hexagons solution
Solution to the Two Regular Hexagons Puzzle
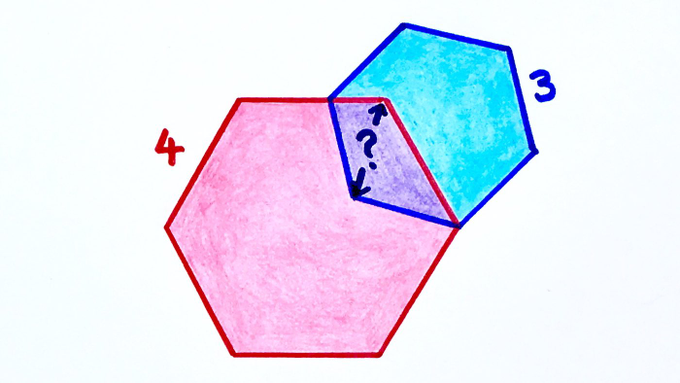
How far apart are the corners of these two regular hexagons?
Solution by the Converse to the Angle at the Circumference is Half the Angle at the Centre
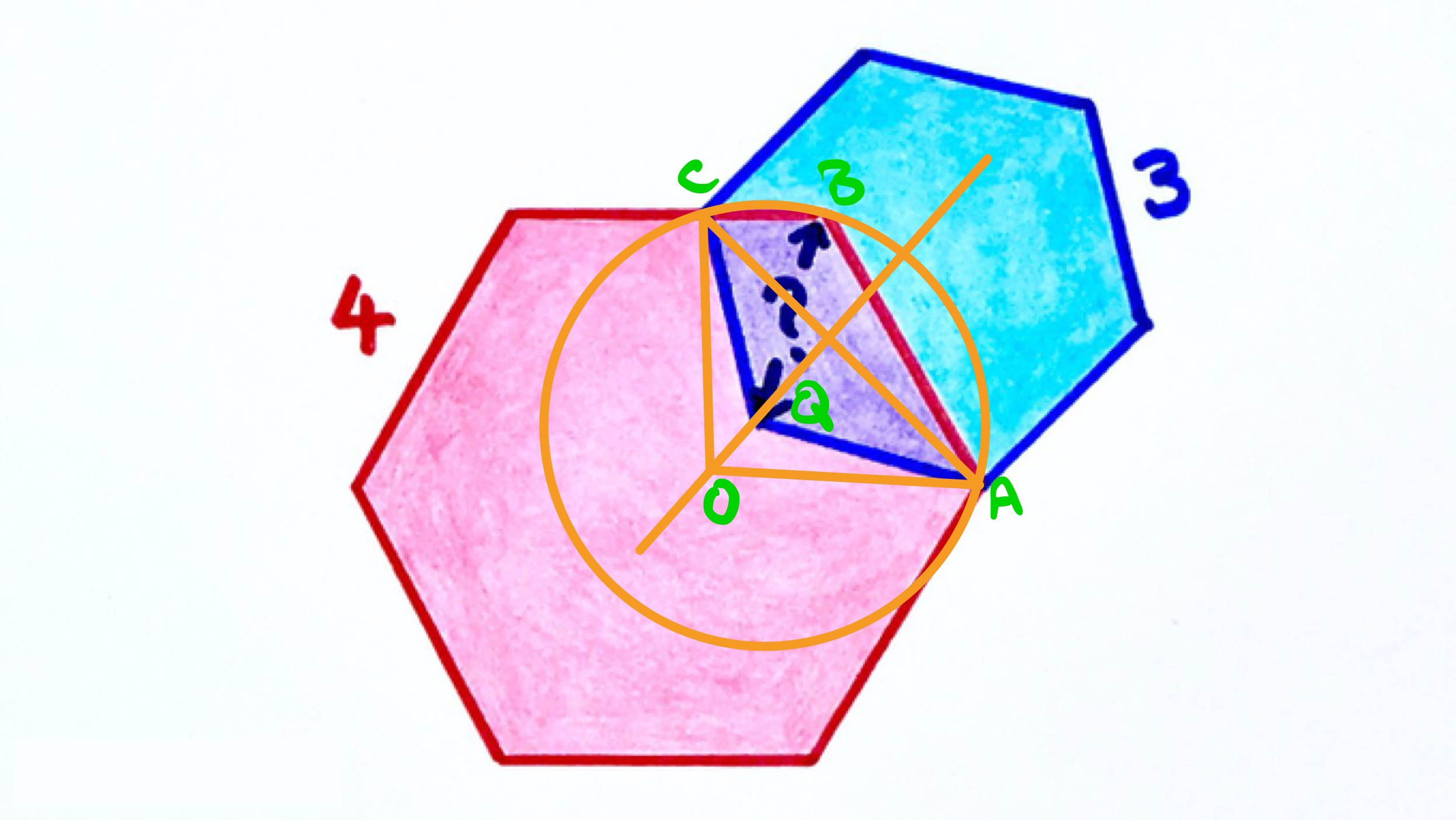
The result that the angle at the circumference is half the angle at the centre has a converse, namely that for a circle and a point not necessarily on the circumference, then if the angle from two points on the circle subtended at the point is half that at the centre then the original point must have been on the circumference after all. As this direction is less well-known, we shall not directly use it but shall effectively prove this result.
With the diagram labelled as above, construct the circumcircle of triangle . The centre of this lies on the perpendicular bisector of each of its sides, in particular on the perpendicular bisector of . Since and are sides of a regular hexagon, they are equal in length and so also lies on this perpendicular bisector.
Angle is as it is the interior angle of a regular hexagon. Therefore, the reflex angle is since the angle at the centre is twice the angle at the circumference. Therefore the non-reflex angle is . But angle is also , so in the quadrilateral , the interior angles at and already account for , leaving nothing left for angles and , meaning both of these angles are and so .
Since , and hence , is the centre of the circumcircle through , , and , the distance is the same as , which is a side of the blue hexagon and hence .
Solution by the Invariance Principle
The problem is actually over-specified. The side length is not needed - the distance is the same regardless of the size of the red hexagon.
Removing that constraint leaves a puzzle where the upper point where the two hexagons meet can slide along the red hexagon’s upper edge, leading to two configurations where the answer can be easily deduced.
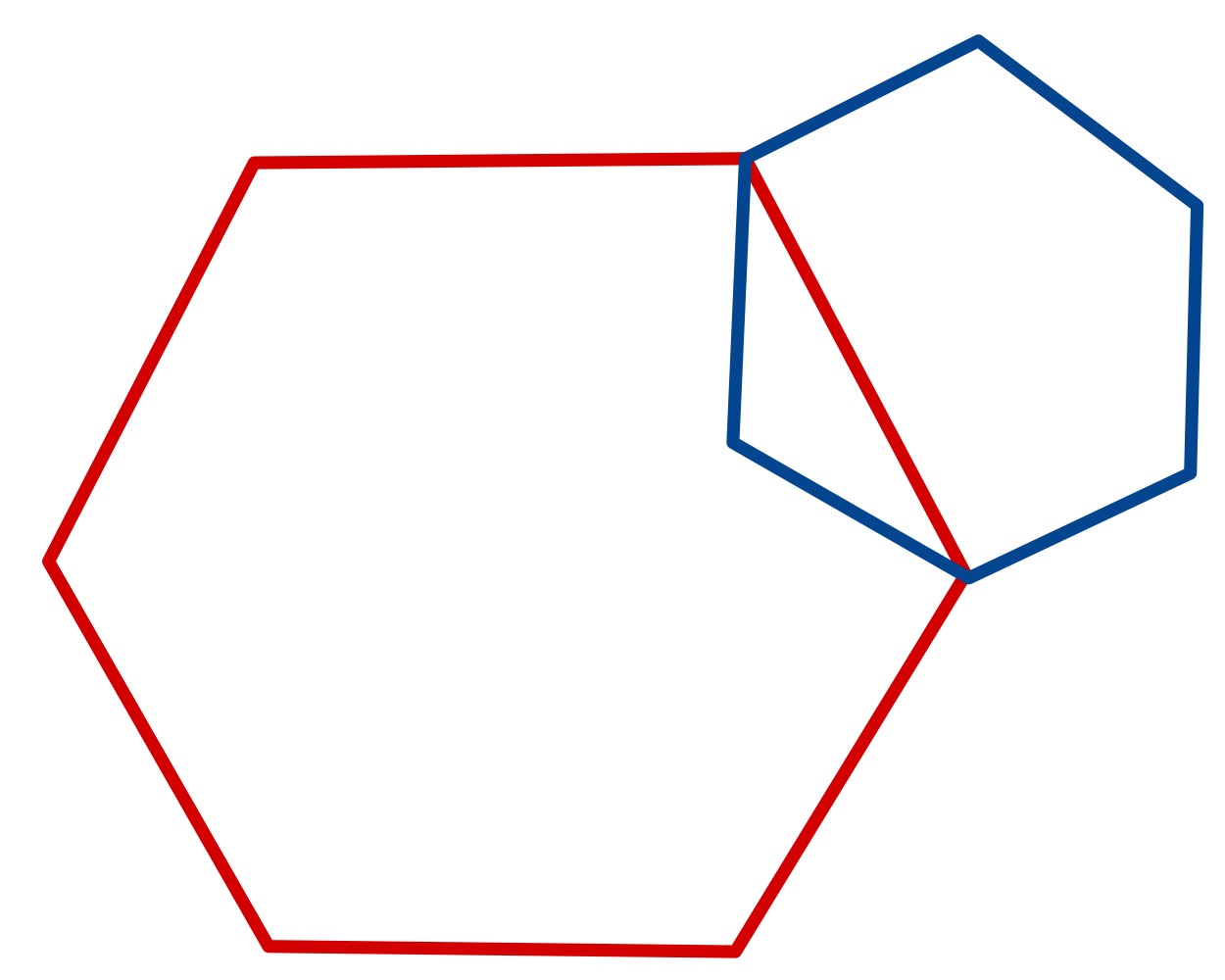
In the first configuration, the meeting point is at the right-hand end of the red hexagon’s edge. The designated corners are then separated by a side of the blue hexagon, hence are apart.
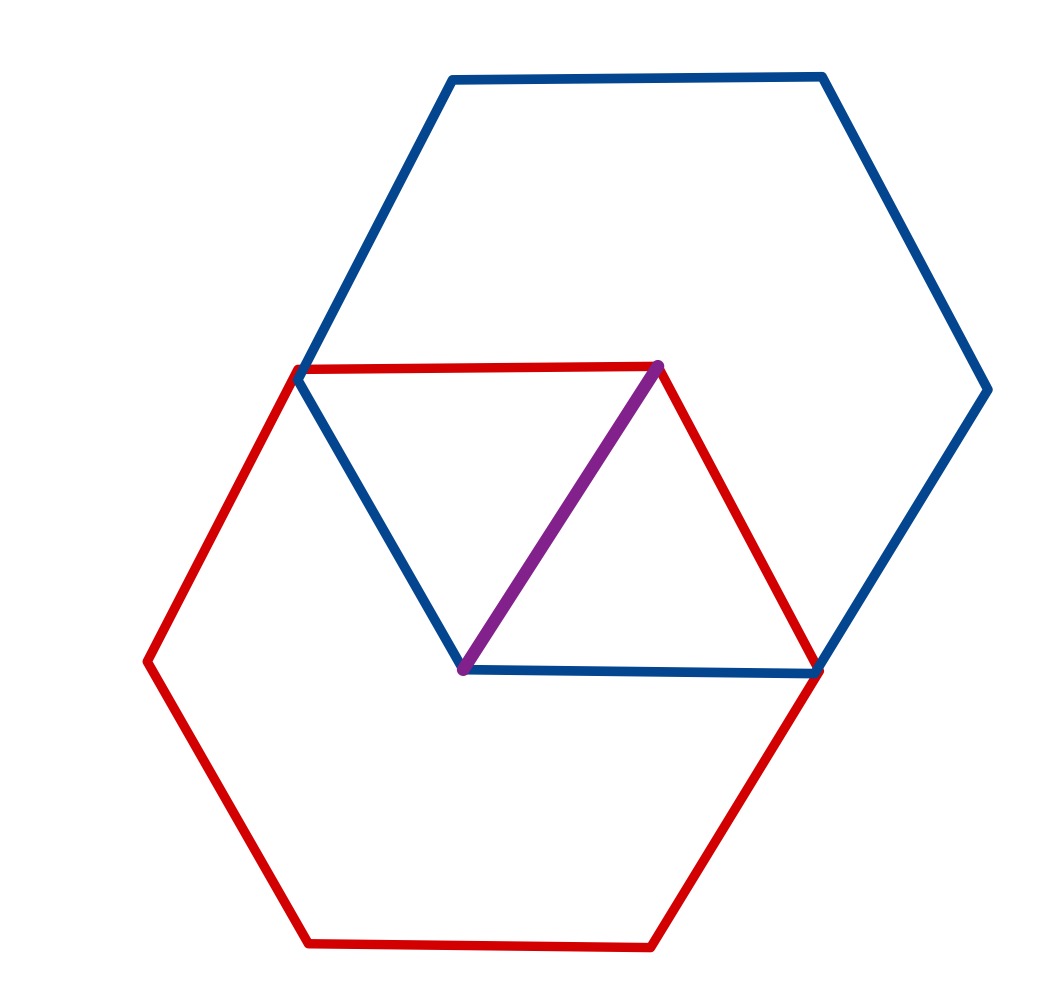
In the second configuration, the meeting point is at the left-hand end of the red hexagon’s edge. The two hexagons are then the same size and the overlap is constructed from two equilateral triangles. The separation of the corners is one side of these triangles, and hence the distance is the same as the side of the blue hexagon, namely .