Notes
tangential hexagon and circle solution
Solution to the Tangential Hexagon and Circle Puzzle
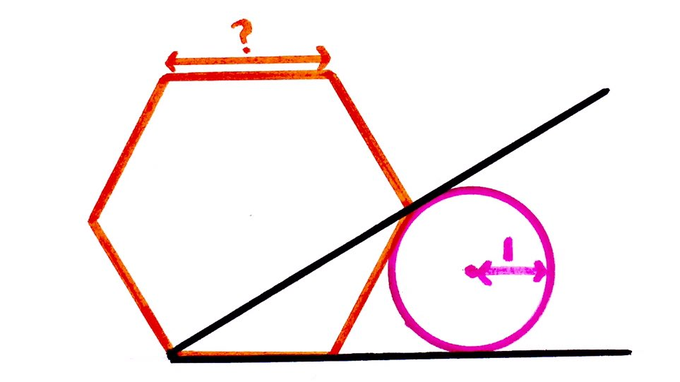
A unit circle is tangent to a regular hexagon. What’s the side length?
Solution by Properties of Isosceles Triangle and Equilateral Triangles, Angles in a Hexagon, Angle Between a Radius and Tangent, and Angles at a Point on a Straight Line
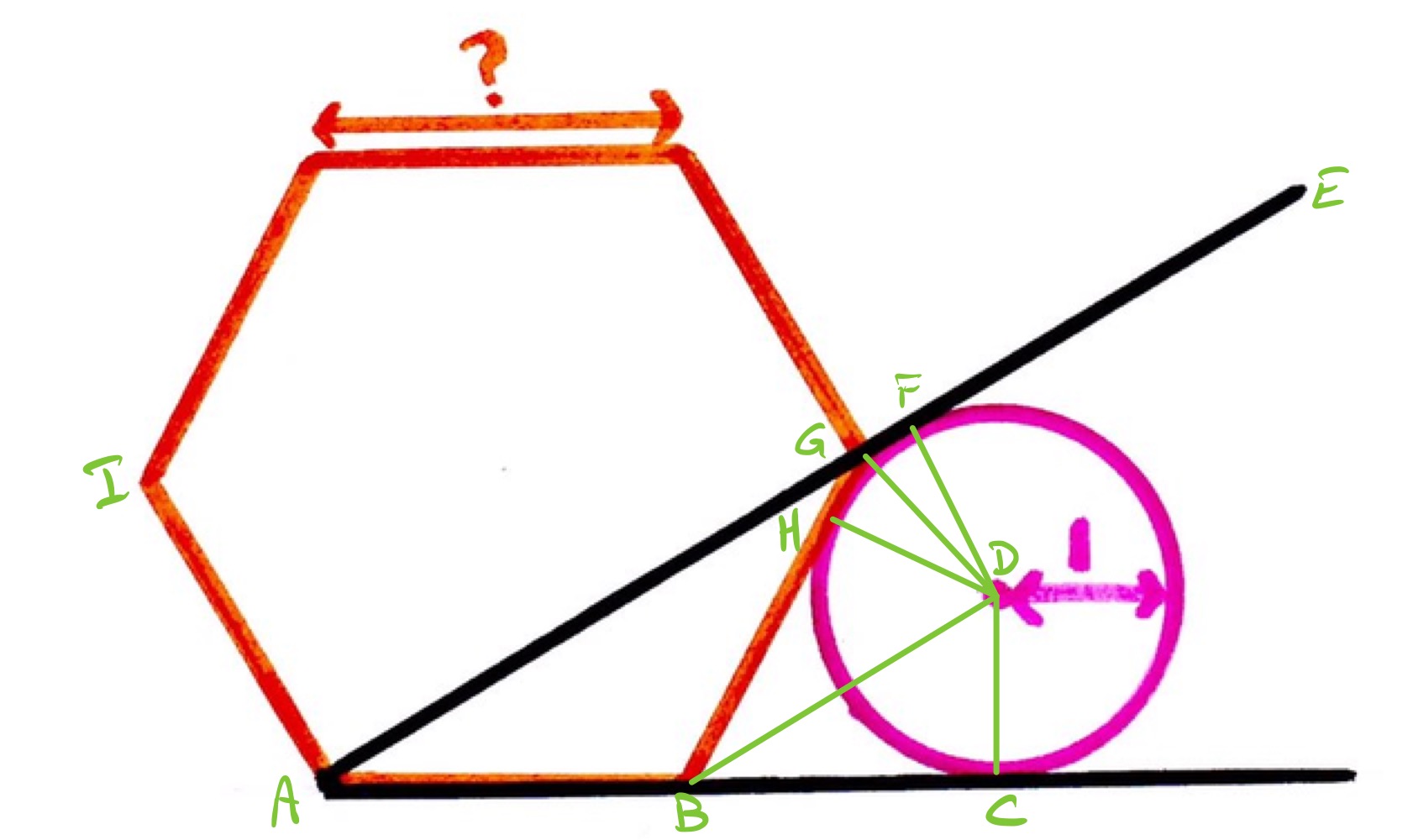
With the diagram labelled as above, triangle is isosceles, and angle as it is the interior angle in a regular hexagon. So angle is . Therefore, angle is by angles at a point on a straight line.
Triangles and are both right-angled and share a side, so are congruent. This means that bisects angle , so angle is . Similarly, angle is as it is the exterior angle of a regular hexagon so angle is .
The angles in triangle are therefore , , and , meaning that it is isosceles. Therefore and have the same length.
Triangle is half an equilateral triangle, so the length of is twice that of , hence is . Therefore has length , and this is the side length of the hexagon.