Notes
seven hexagons solution

Solution to the Seven Hexagons Puzzle

Solution by Lengths in a Regular Hexagon and Pythagoras' Theorem

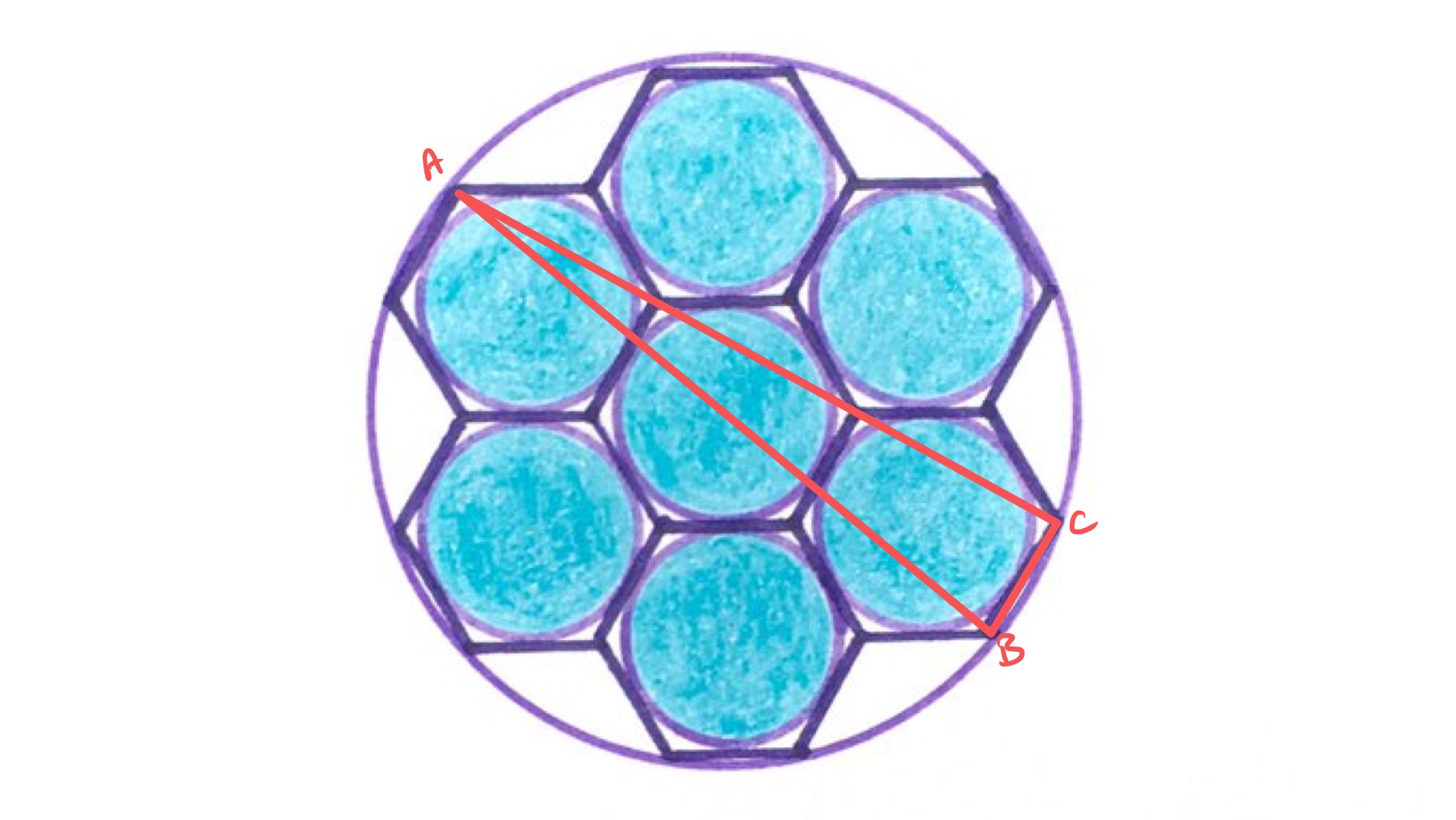
In the diagram above, let $x$ be the side length of one of the hexagons. Using the calculations on lengths in a regular hexagon, the line segment $A C$ has length $3\sqrt{3} x$. Applying Pythagoras' theorem to triangle $A B C$ shows that the length of $A B$ is $\sqrt{28}x$. This is the diameter of the large circle so its area is $7 \pi x^2$. The diameter of the smaller circles is the same as the shorter diameter of the hexagons, namely $\sqrt{3} x$, so their combined area is $7 \times \pi \frac{3}{4} x^2 = \frac{3}{4} \times 7 \pi x^2$. Therefore, $\frac{3}{4}$ of the large circle is shaded.