Notes
two triangles overlapping a quarter circle solution
Solution to the Two Triangles Overlapping a Quarter Circle Puzzle
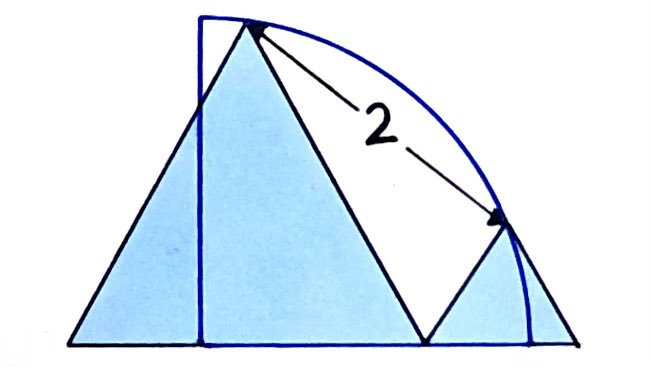
Both triangles are equilateral. What’s the area of the quarter circle?
Solution by Angle at the Centre is Twice the Angle at the Circumference
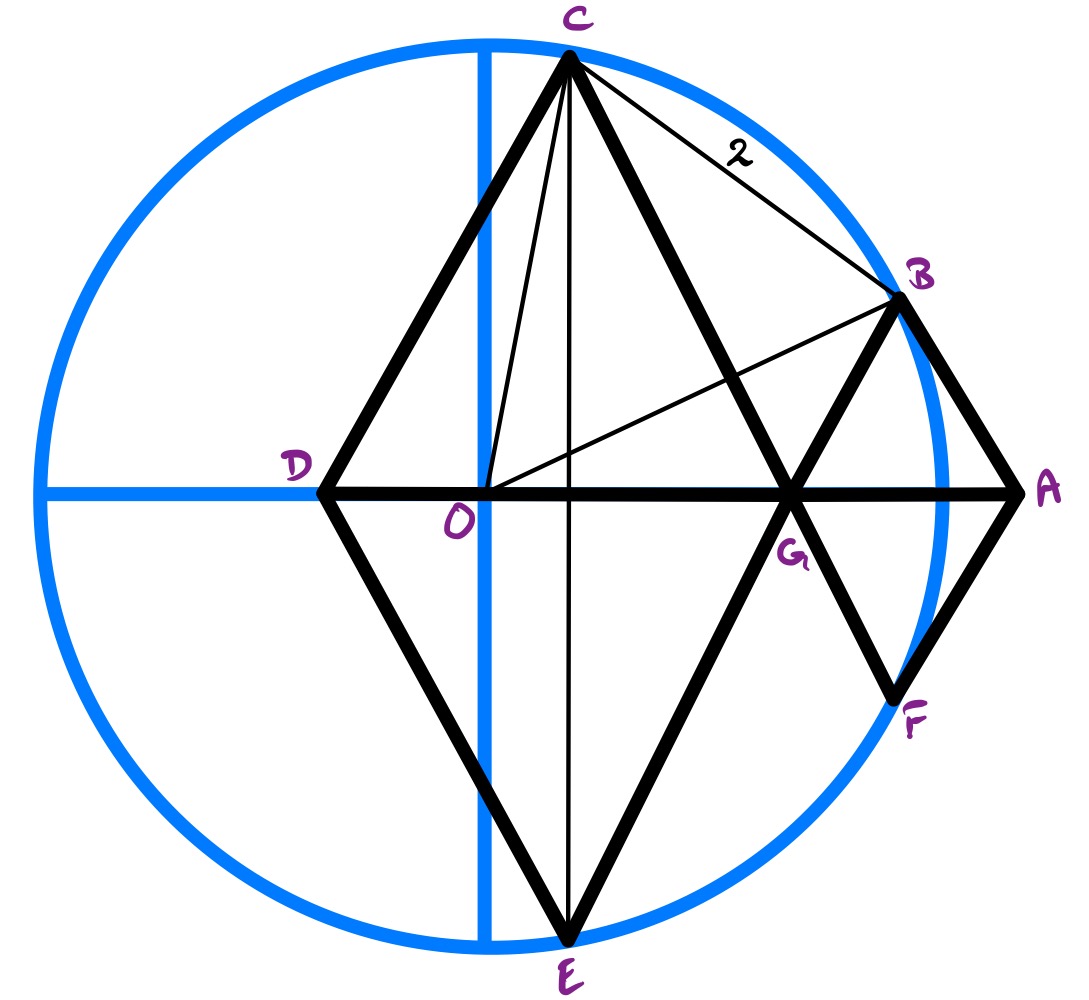
Consider the above diagram, in which the quarter circle is extended to a full circle and the two equilateral triangles are reflected in the horizontal diameter.
The shape is formed by two equilateral triangles and so has all four sides the same length, therefore it is a rhombus. The line segment therefore bisects angle so the angle formed, namely , is .
The angles formed at are all , so forms a straight line. Therefore, angle is the same as angle . Then as the angle at the centre is twice the angle at the circumference, angle is . Since triangle is made from two radii of the circle it is at least isosceles, but then as it must be equilateral. Therefore the radius of the circle has length .
The area of the quarter circle is therefore .
Solution by Agg Invariance Principle
The sizes of the two triangles are not specified, so can be adjusted.
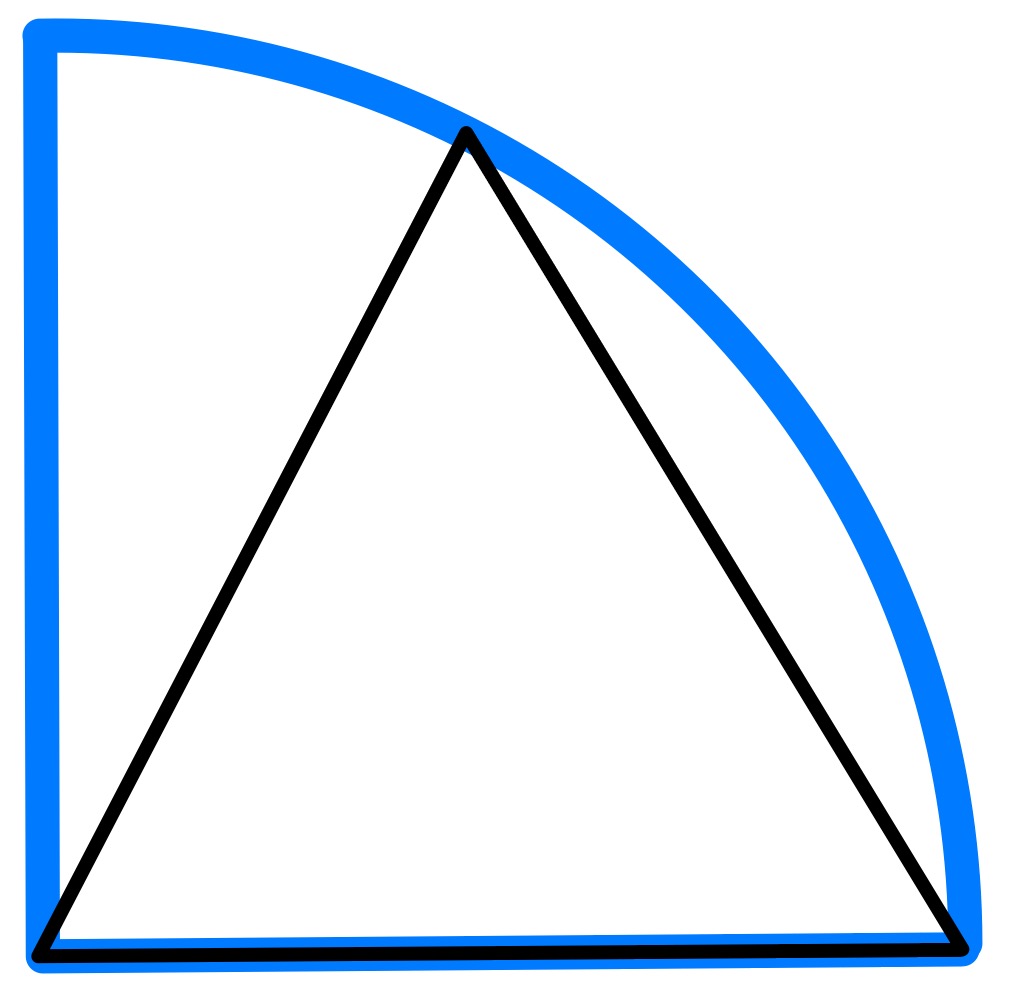
In this version, the right-hand triangle is shrunk down to a point. Then the lower right vertex of the left-hand triangle is on the circumference of the circle, as is its upper vertex. The chord formed by the edge of the triangle is at to the radius, and so forms part of a hexagon. This shows that the third vertex of the equilateral triangle is at the centre. The radius of the quarter circle is then the same as the side length of the triangle, which is . Hence the area of the quarter circle is .