Notes
two regular hexagons ii solution
Solution to the Two Regular Hexagons (II) Puzzle
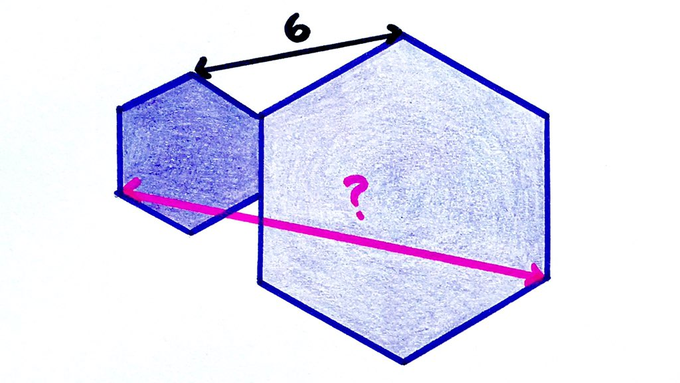
Both hexagons are regular. How long is the pink line?
Solution by Lengths in a Regular Hexagon and Similar Triangles
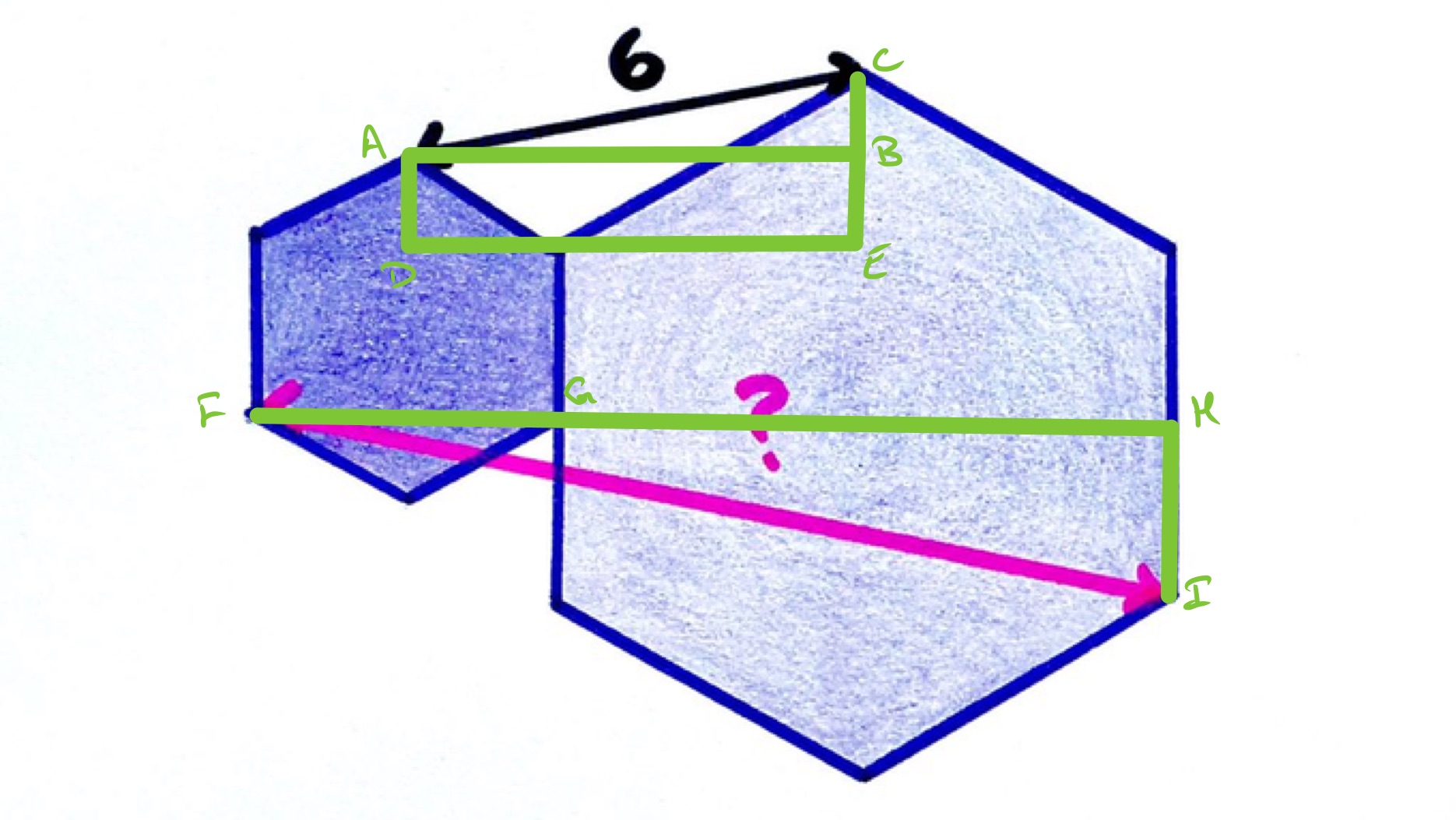
Consider the triangles and in the diagram. The length of is half the length of . The length of is the difference of the sides. Using lengths in a regular hexagon, and have lengths half the side lengths of their respective hexagons, so the length of is half the difference of these sides and so has half the length of . Since both and are right-angled triangles, this establishes them as similar with a scale factor of . Therefore the length of is twice that of and so is of length .
Solution by Invariance Principle
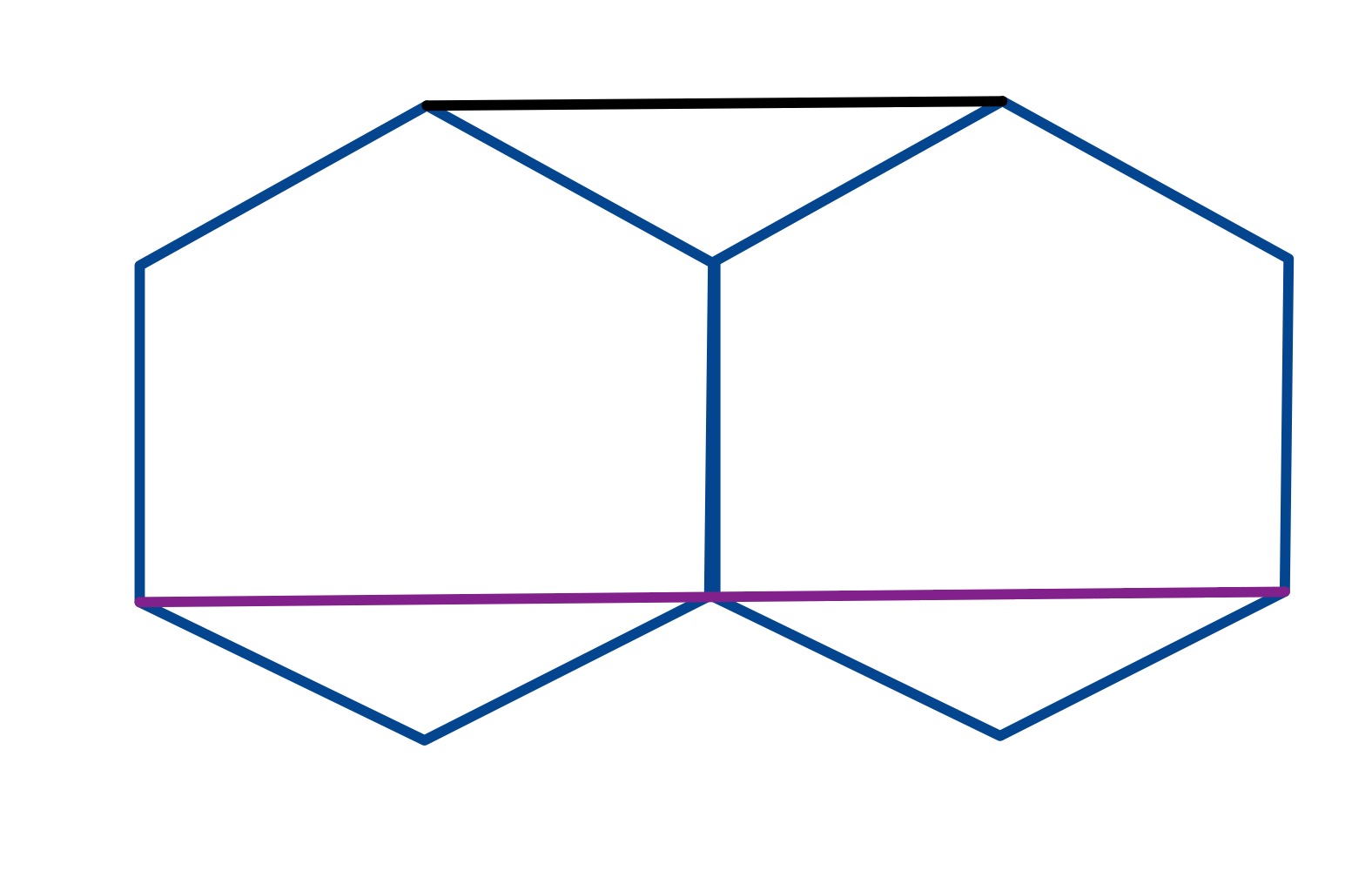
By drawing the hexagons the same size, the relationship between the two lengths is clear and so the required length is .