Notes
two quarter circles in a semi-circle ii solution
Solution to the two quarter circles in a semi-circle ii puzzle
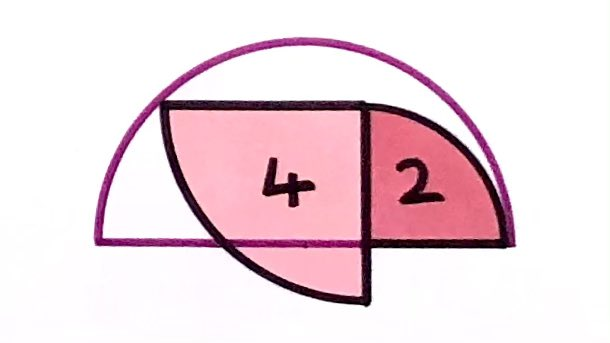
The areas of the quarter circles are given. What’s the area of the semicircle?
Solution Using Circle Theorems
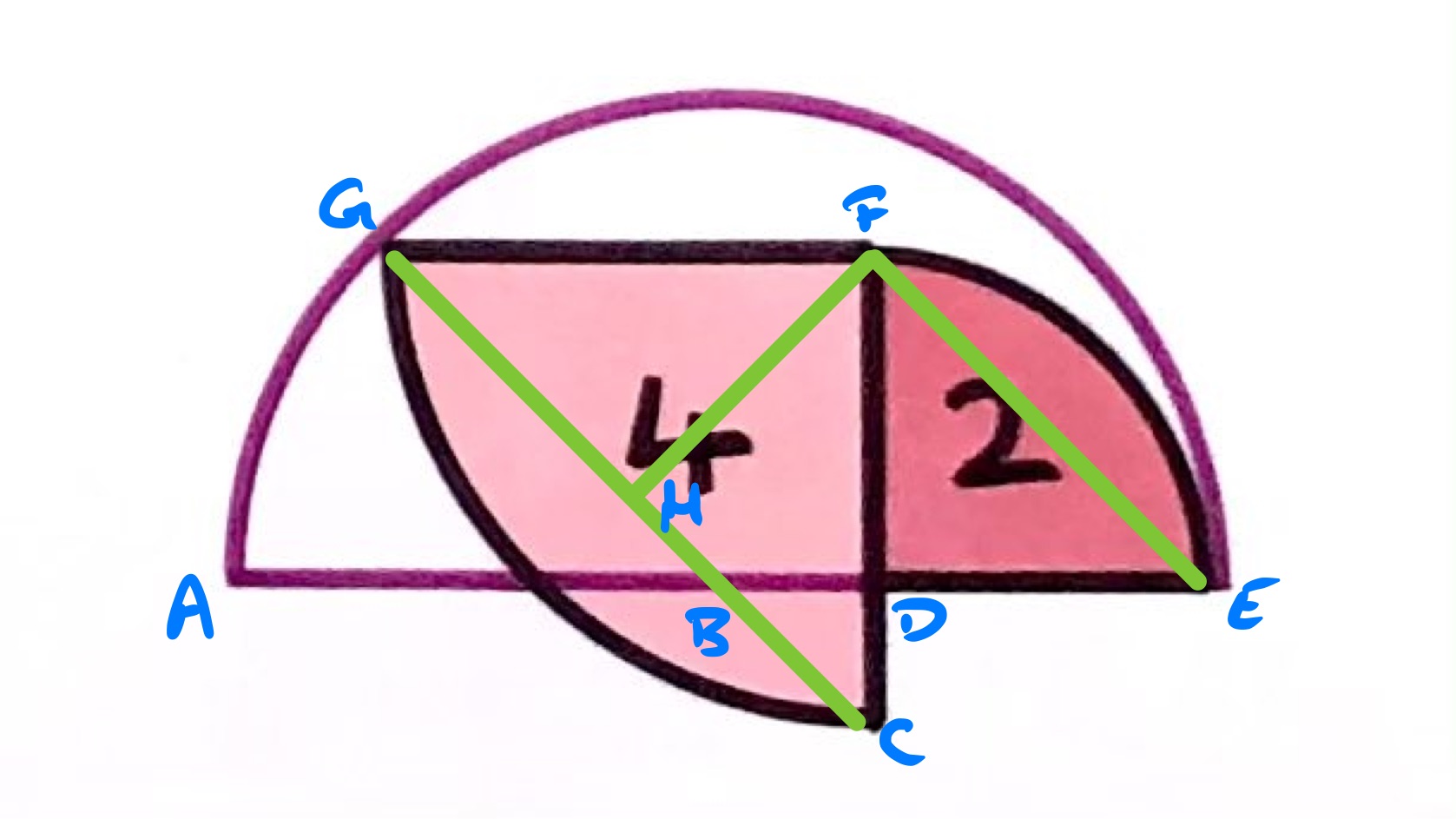
To find the area of the semi-circle, we need to locate its centre. There are a couple of different ways to do this, but all start with drawing the diagonals of the quarter circles.
Since the larger quarter circle is twice the size of the smaller, so also is the larger triangle, in the diagram, twice the size of the smaller, . We can therefore fit two copies of inside , as and . This shows that the length of is the same as the length of . (This can also be shown using Pythagoras' Theorem together with the area scale factor.)
Angle at centre is twice angle at circumference
Having established that , triangle is isosceles with angle . So angle and also . Then angle and hence is the centre of the circle.
Symmetry
The quadrilateral is a parallelogram with and so is a rhombus. Its diagonals are therefore perpendicular bisectors of each other. Since is a chord of the circle, the centre of the circle lies on its perpendicular bisector which is (the extension of) . As is a diameter, the intersection of and is therefore the centre of the circle, and this is .
Calculating the Area
Once is established as the centre, calculating the area goes as follows. Since is the centre, is a radius. This is equal in length to , which is equal to . The radius of the semi-circle is therefore the same as the radius of the larger quarter circle and so the area of the semi-circle is .