Notes
two overlapping triangles and a circle solution
Solution to the Two Overlapping Triangles and a Circle Puzzle
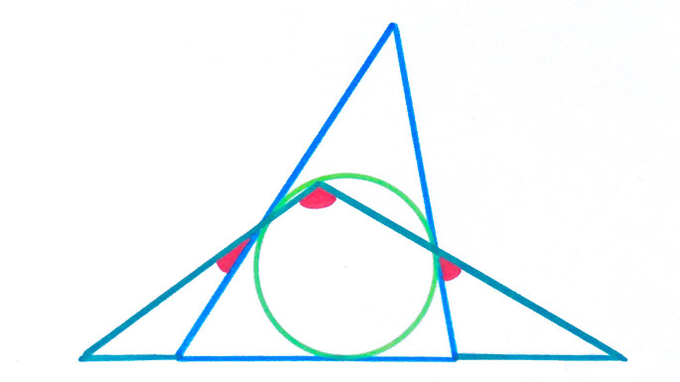
What’s the sum of these three angles?
Solution by Vertically Opposite Angles, Alternate Segment Theorem, and Angles in a Triangle
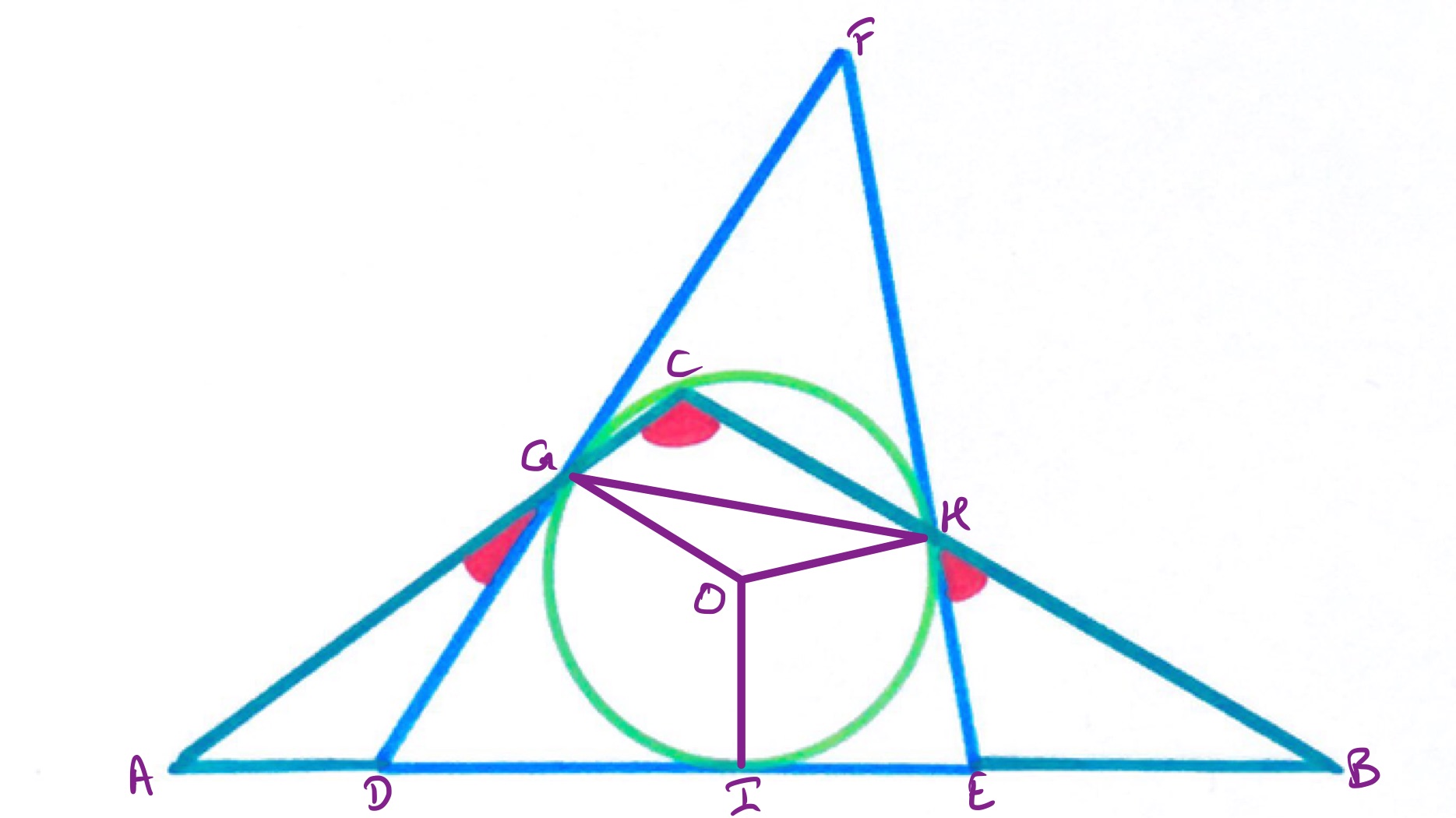
With the points labelled as above, angles and are equal as they are vertically opposite, then angles and are equal by the alternate segment theorem. So angle is equal to angle . By a similar argument, angle is equal to angle . Angles , , and are the three angles interior to triangle and so sum to .
Solution by Angles in a Quadrilateral, Angle at the Centre is Twice the Angle at the Circumference, Angle Between a Radius and Tangent
With the points labelled as above, let us write for angle , for angle , and for angle .
The anti-clockwise angle is twice angle as the angle at the centre is twice the angle at the circumference, so is . So the anti-clockwise angle is .
Angles and are as they are both the angles between a radius and tangent. So in quadrilateral , angle is .
Angle is equal to angle , so is , as they are vertically opposite angles. Similarly, angle is equal to .
The angle sum of quadrilateral is then . Since the sum of the angles in a quadrilateral is , this shows that .
Solution by Invariance Principle
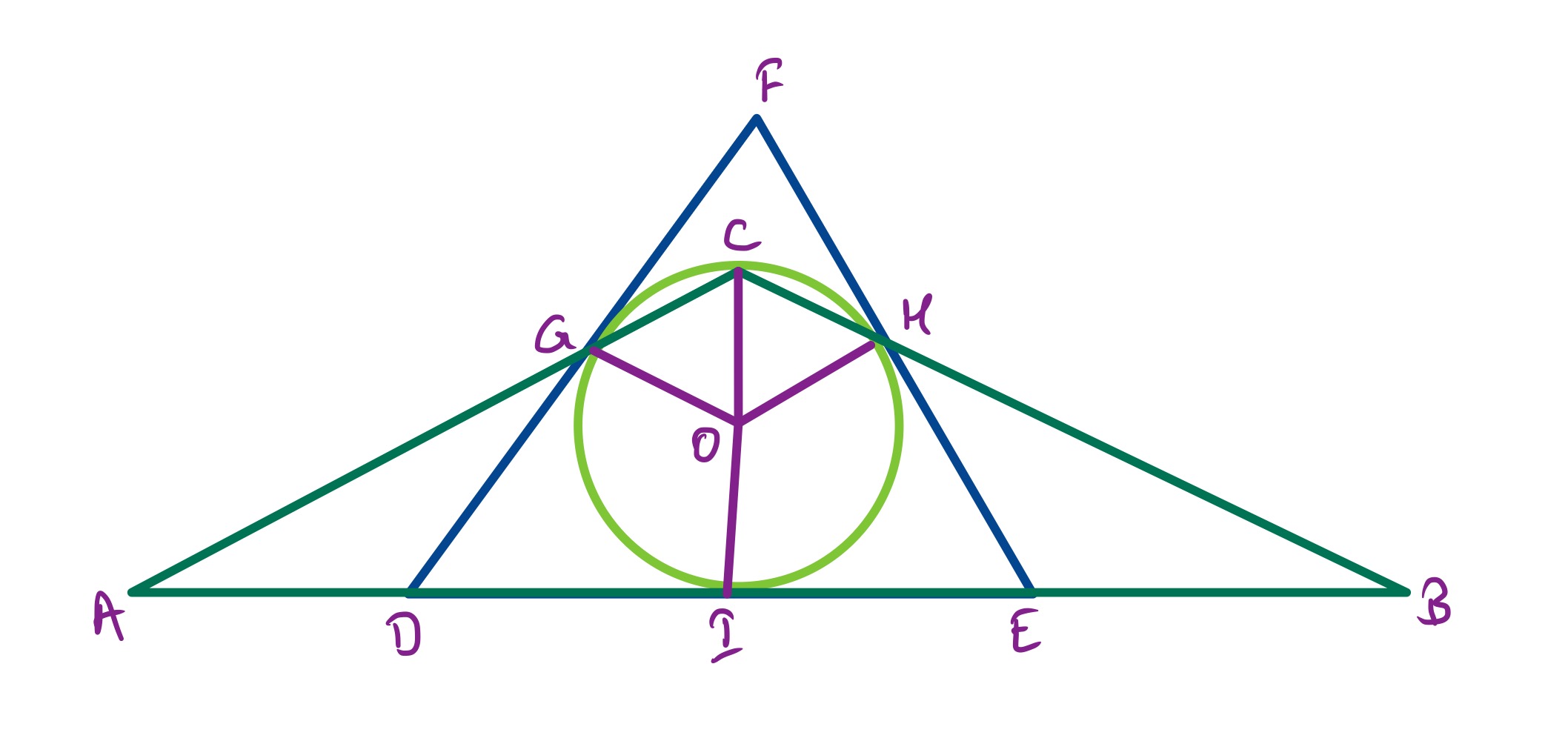
In the above configuration, triangle is equilateral. Angle is , so triangles and are also equilateral making angle equal to . Triangle is isosceles meaning that angles and are . Angles and are , meaning that angles and are . So the marked angles sum to .