Notes
two overlapping hexagons and a rectangle solution
Solution to the Two Overlapping Hexagons and a Rectangle Puzzle
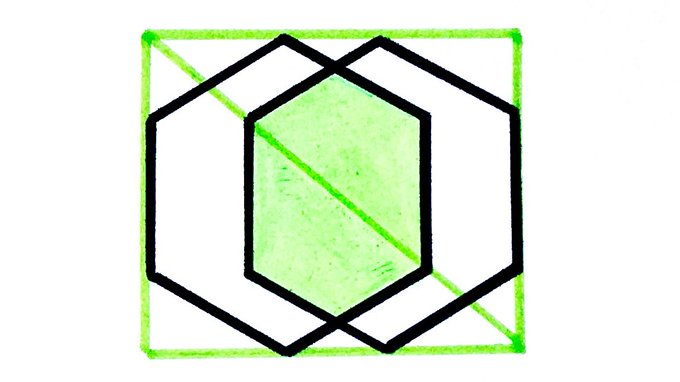
One corner of each regular hexagon lies on the diagonal of the rectangle. What fraction of the rectangle is shaded?
Solution by Similarity and Lengths in a Regular Hexagon
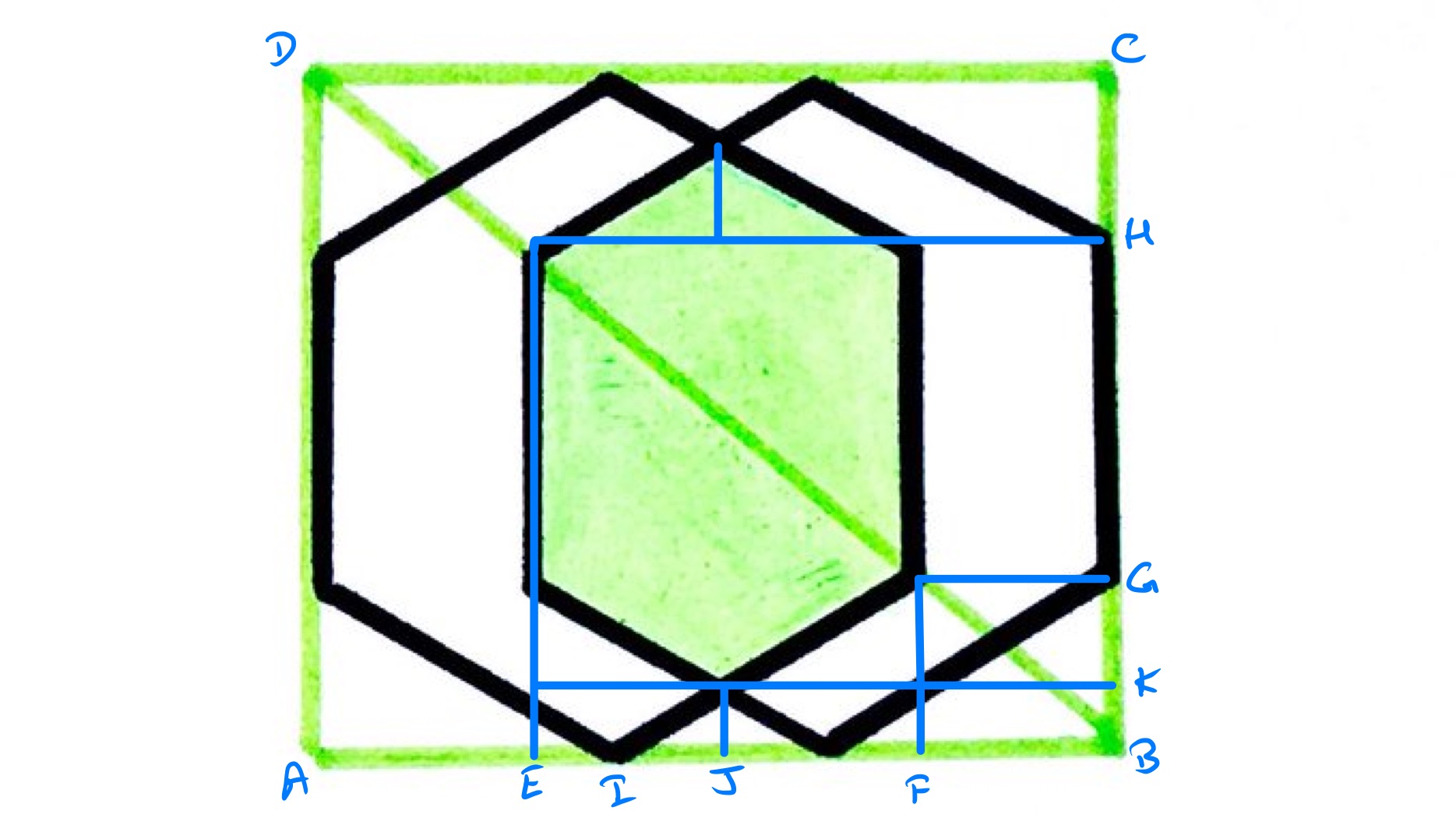
The two triangles at the top of the shaded region are congruent to the two white triangles below it, showing that the area of the shaded region is the same as the area of the rectangle with height parallel to and width parallel to .
The height of the outer rectangle, which is the length of , is the larger diameter of the hexagons, which is twice a side length. Thus the length of is twice that of . The points and correspond to and along , so is half of and is located centrally along that edge.
So along , is at the midpoint, while is at the midpoint of and of . Point is at the midpoint of . So the points along lie at the following locations (as proportions of ): is at , at , at , and at . This means that is one third of the way between and , so is one third of the way from to . Since is one quarter of , is two thirds of one quarter of , which is .
As a proportion of then is while is of . So the shaded region has area equal to of the area of the outer rectangle.