Notes
two hexagons and a square solution

Solution to the Two Hexagons and a Square Puzzle

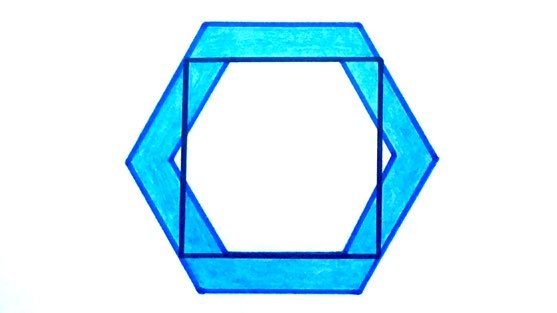
Two Hexagons and a Square

Two regular hexagons, and a square of side length $2$ . What’s the shaded area?

Solution by Lengths in a Regular Hexagon

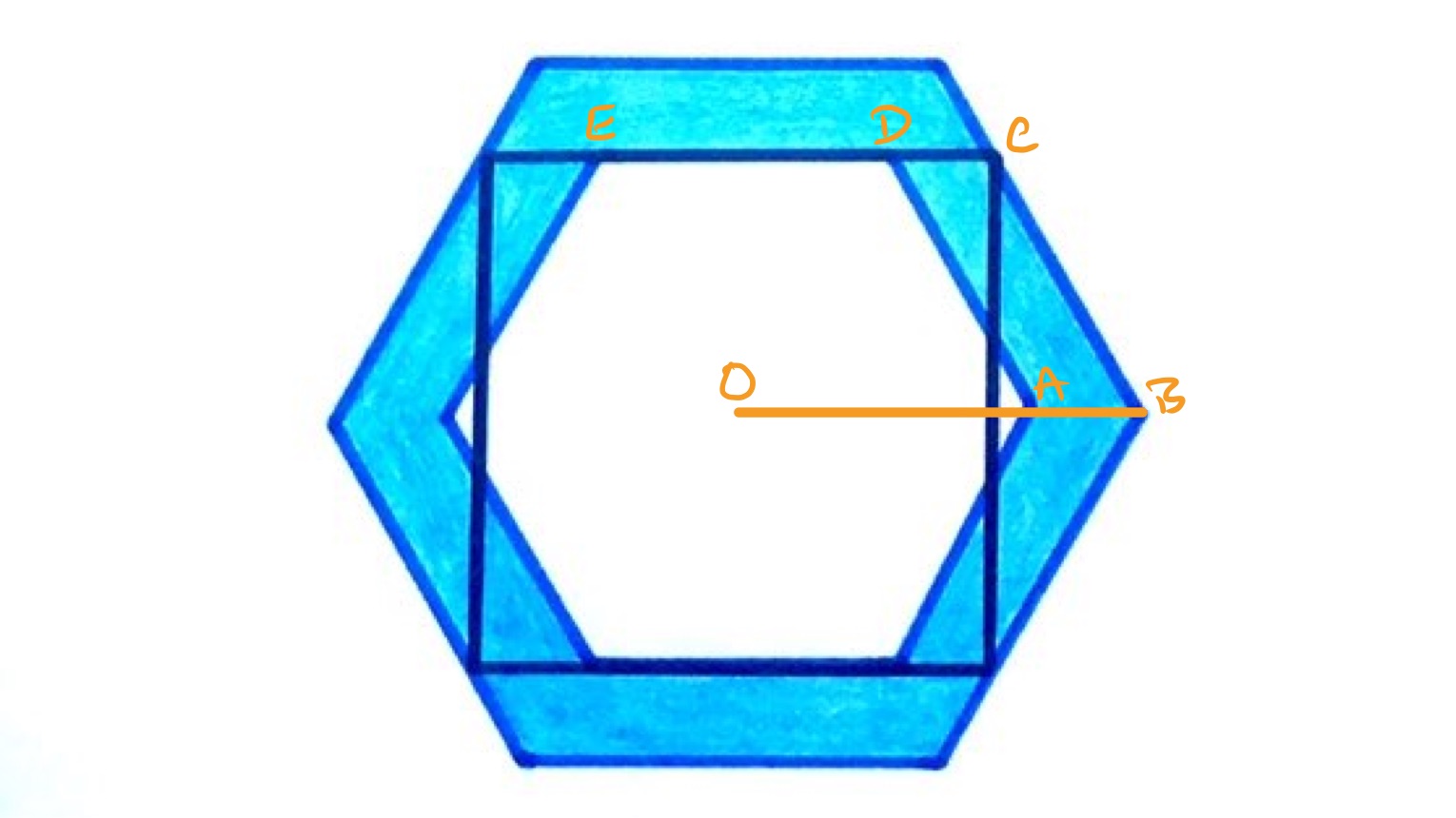
Two hexagons and a square labelled

The side length of the square is the same as the smaller diameter of the inner hexagon, which is $\sqrt{3}$ times the side length. So the side length of the inner hexagon is $\frac{2}{\sqrt{3}}$ . The excess $C D$ is half of what is left over, so has length:

\frac{1}{2} \left(2 - \frac{2}{\sqrt{3}}\right) = 1 - \frac{1}{\sqrt{3}}

This is the same as the length of $A B$ . Since the length of $O A$ is the same as the side length of the inner hexagon, the length of $O B$ , which is the same as the side length of the outer hexagon, is:

\frac{2}{\sqrt{3}} + 1 - \frac{1}{\sqrt{3}} = 1 + \frac{1}{\sqrt{3}}

The area of a hexagon is $\frac{3\sqrt{3}}{2}$ times the square of its side length, so the area of the shaded region is:

\frac{3\sqrt{3}}{2} \left( \left(1 + \frac{1}{\sqrt{3}}\right)^2 - \left(1 + \frac{1}{\sqrt{3}}\right)^2 \right) = 6

Created on August 21, 2021 21:20:22 by Andrew Stacey

Notes two hexagons and a square solution

Solution to the Two Hexagons and a Square Puzzle

Solution by Lengths in a Regular Hexagon

Notes
two hexagons and a square solution