Notes
trisected hexagon solution
Solution to the Trisected Hexagon Puzzle
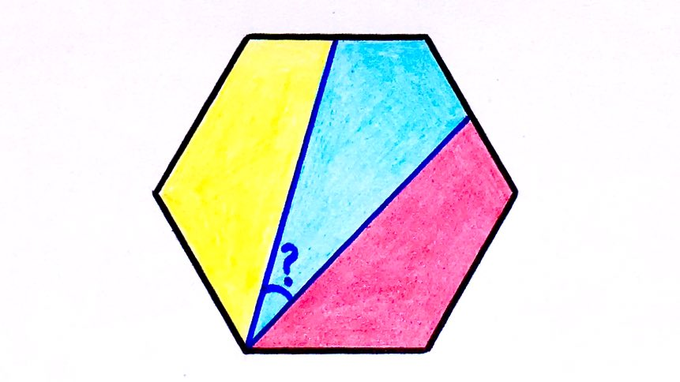
This regular hexagon has been split into thirds. What’s the angle?
Solution by Trigonometry, Regions in a Regular Hexagon, and Area of a Triangle
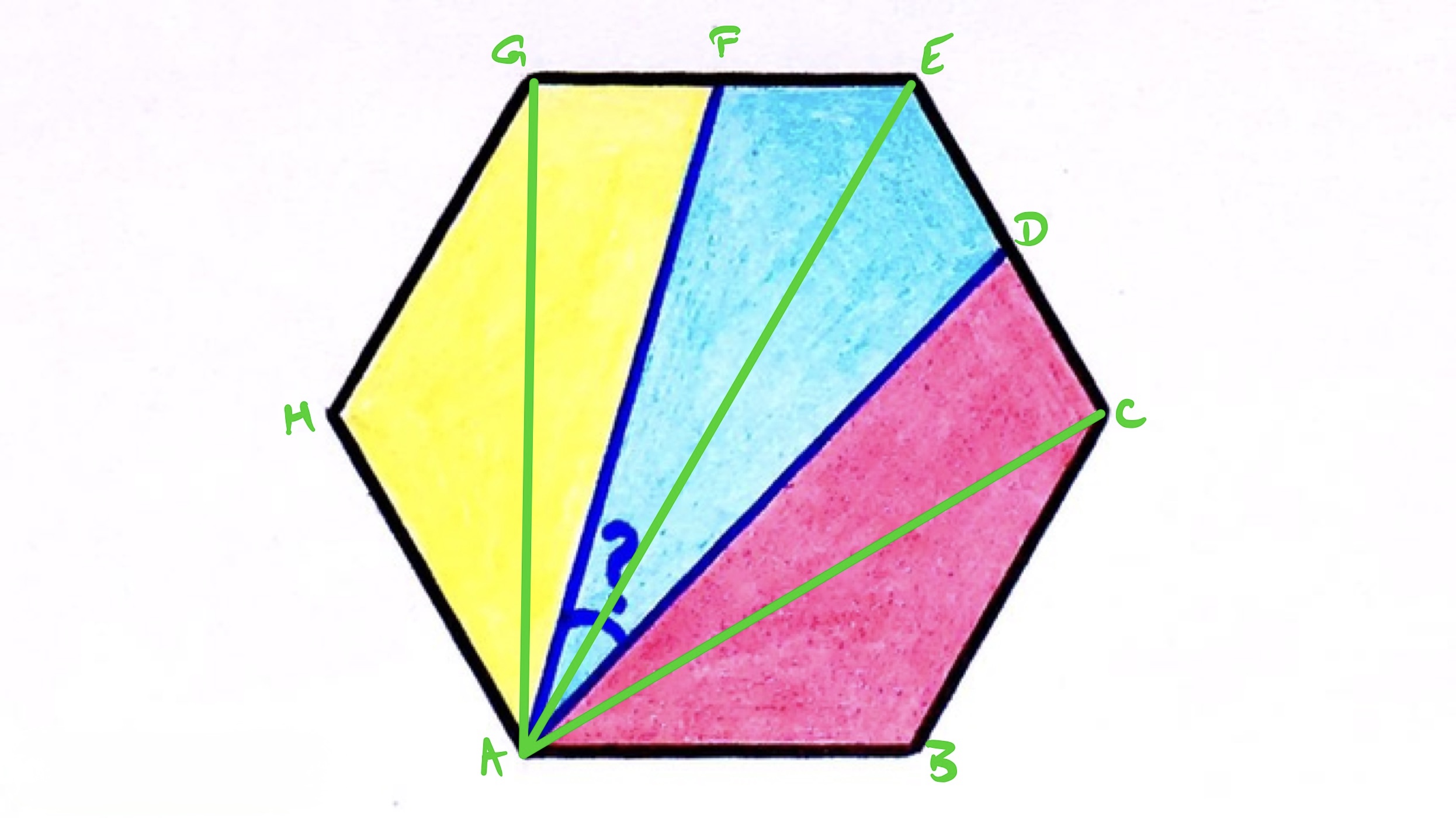
With the points labelled as above, the regions and are each one sixth of the hexagon. Therefore, the triangle is one sixth of the hexagon. Triangle is half of the blue region so is also one sixth of the hexagon. Therefore, by the area of a triangle, triangles and must have the same “base”, so and have the same length.
Angle can then be computed using trigonometry, since has length times that of , so angle is given by . Then angle is the same, and so since angle , we have that angle is (to decimal places):