Notes
triangles in a dodecagon solution

Solution to the Triangles in a Dodecagon Puzzle

Solution by Regions in a Regular Hexagon and Equilateral Triangle

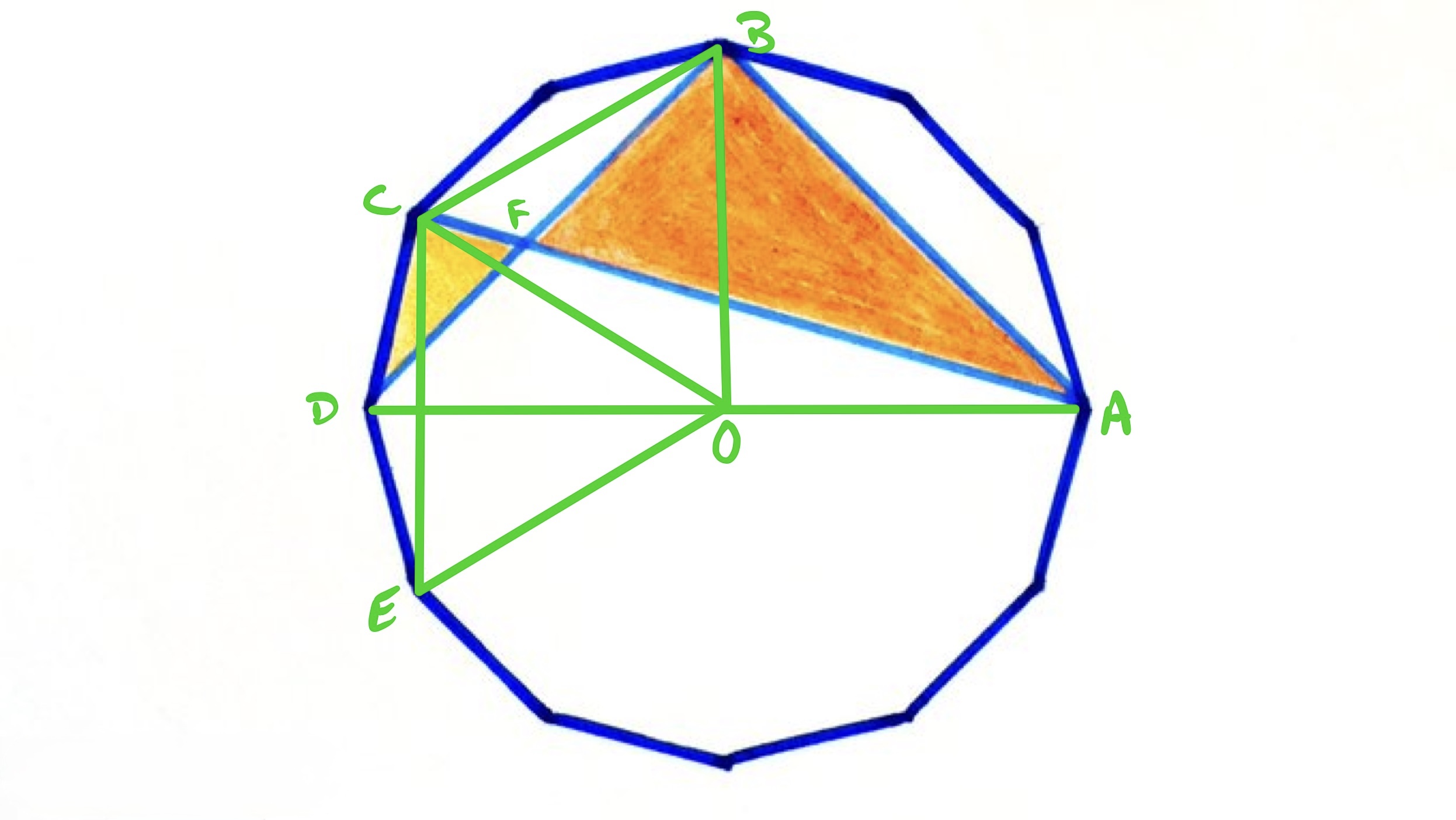
Label the points as above, so $A D$ is a diameter of the dodecagon and $O$ is its centre. Joining every other vertex creates a regular hexagon and so triangle $O C E$ is an equilateral triangle, meaning that $C E$ has the same length as $O C$ and hence as $O B$. The height of $C$ above $A D$ is therefore half of that of $B$ above it, so using the area of a triangle, triangle $A C D$ has half the area of triangle $A B D$.

Triangle $A B D$ consists of the orange region plus triangle $A F D$, and triangle $A C D$ consists of the yellow region plus triangle $A F D$. Since the orange region is $2$ more than the yellow, this means that the area of triangle $A B D$ is $2$ more than that of triangle $A C D$. Since triangle $A C D$ has half the area of triangle $A B D$, this means that triangle $A C D$ has area $2$.

Then as $O$ is the midpoint of $A D$, triangle $O C D$ has half the area of $A C D$, namely $1$. The dodecagon is made up of $12$ triangles congruent to $O C D$ and so has total area $12$.