Notes
triangle overlapping a hexagon solution
Solution to the Triangle Overlapping a Hexagon Puzzle
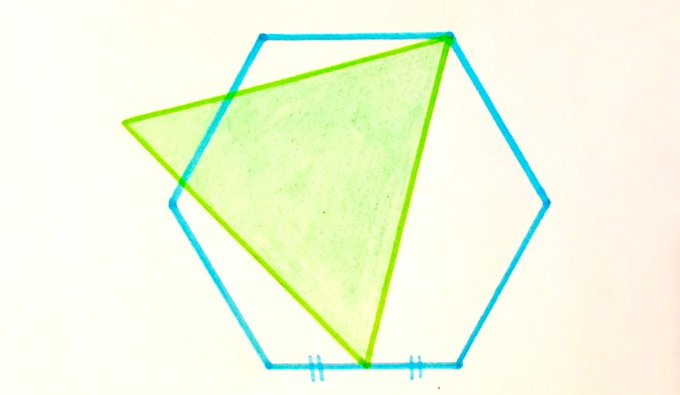
If the area of the regular hexagon is , what’s the area of the equilateral triangle?
Solution by Pythagoras' Theorem and Properties of Regular Hexagons and Equilateral Triangles
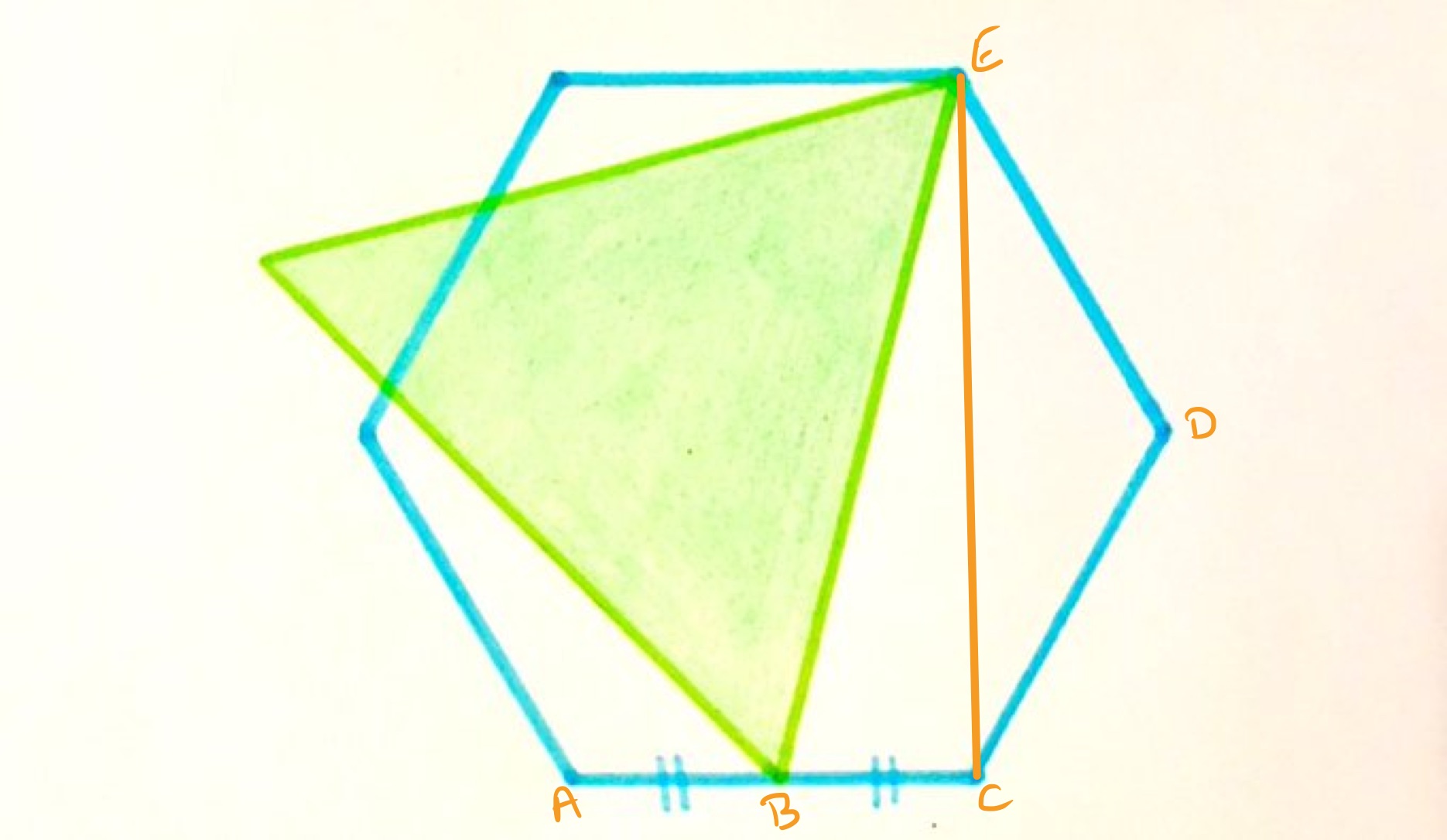
Let be the length of one of the sides of the hexagon and let be the length of one of the sides of the triangle. Then using lengths in a regular hexagon, the length of in the diagram is . Applying Pythagoras' theorem to triangle shows that:
From regular hexagon, the area of the hexagon is and from equilateral triangle, the area of the triangle is . So and
Hence the area of the equilateral triangle is .