Notes
triangle in circle in triangle in semi-circle solution

Triangle in Circle in Triangle in Semi-Circle

Solution by Angle in a Semi-Circle and Alternate Segment Theorem

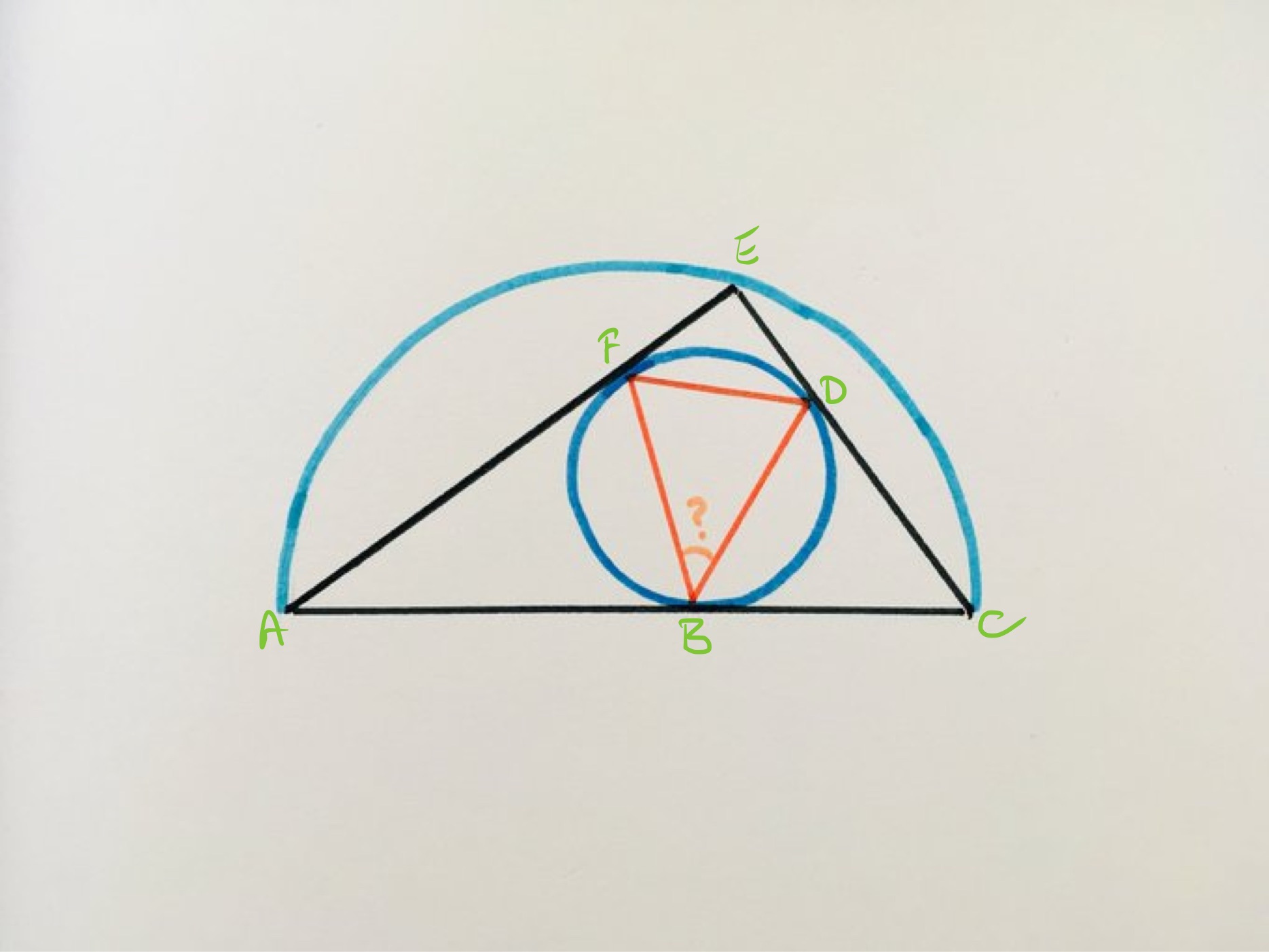
With the points labelled as above, angle $A \hat{E} C$ is the angle in a semi-circle so is a right-angle. As $A E$ and $C E$ are both tangent to the smaller circle, $F E$ and $E D$ are the same length, so triangle $F E D$ is isosceles and right-angled. Therefore, angle $D \hat{F} E$ is $45^\circ$. By the alternate segment theorem, angle $D \hat{B} F$ is also $45^\circ$.