Notes
three triangles and a rectangle inside a circle solution
Solution to the Three Triangles and a Rectangle Inside a Circle Puzzle
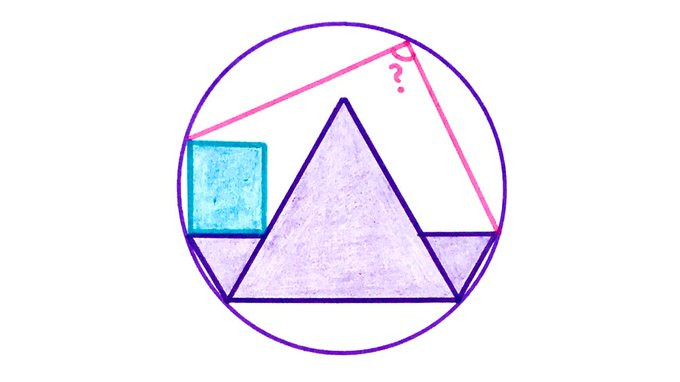
Three equilateral triangles and a rectangle are stacked up inside this circle. What’s the angle?
Solution by Symmetry and Angle in a Semi-Circle
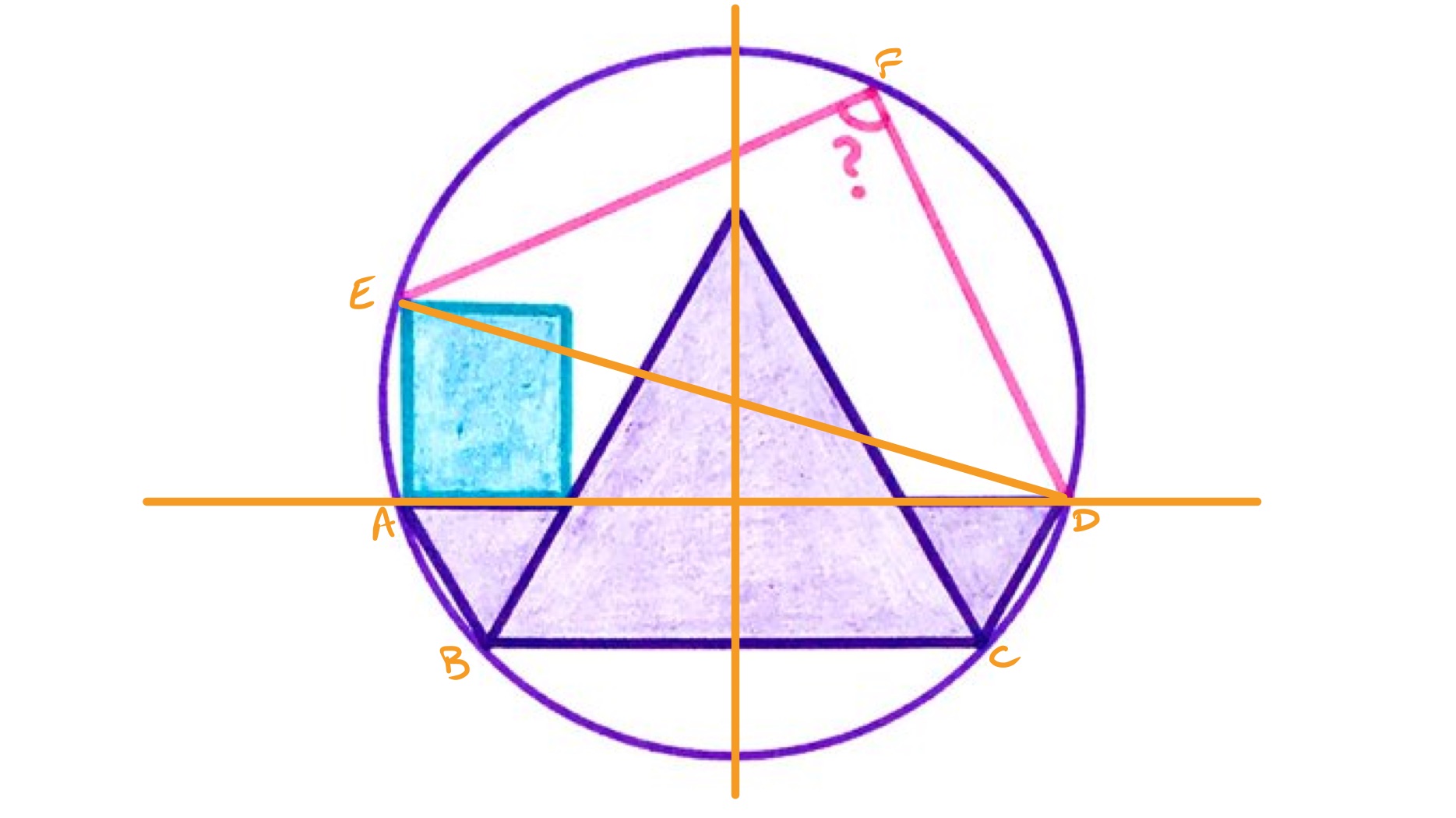
In the diagram above, the vertical line through the midpoint of chord passes through the centre of the circle. It is therefore a line of symmetry of both the circle and the central equilateral triangle. Since the points and depend on the circle and the central equilateral triangle, reflecting in the vertical line swaps and and so in particular the line joining to is the continuation of their horizontal sides. This establishes angle as a right-angle, and so is a diameter of the circle since the angle in a semi-circle is a right-angle. By the same result, angle is then also a right-angle.