Notes
three right-angled triangles solution
Three Right-Angled Triangles
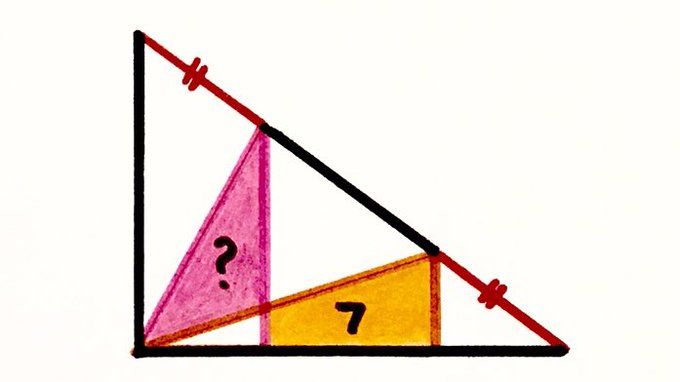
This pattern is made from three right angled triangles. The two red lengths are equal. What’s the pink area?
Solution by Area of a Triangle and Corresponding Angles
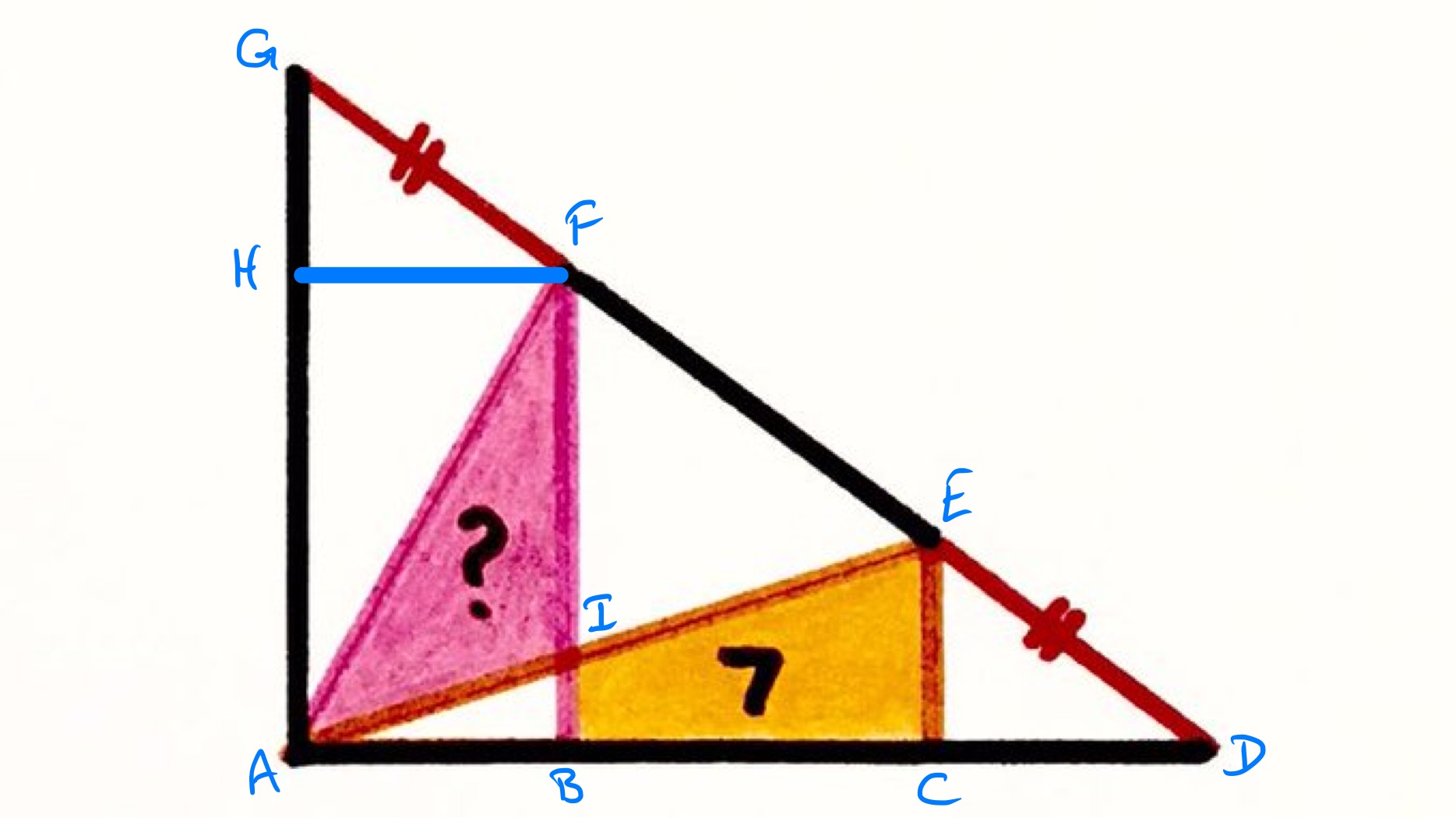
In the above diagram, the point labelled is such that is parallel to .
Consider the two triangles and . The lengths of and are given to be the same, and the “height” of above these two “bases” is the same, so their area is the same. As triangles and are both right-angled, have the same length hypotenuse, and angles and are corresponding angles, these two triangles are congruent and so have the same area. Therefore triangles and have the same area.
Quadrilateral is a rectangle since is parallel to and angle is a right-angle, so triangles and have the same area.
Therefore triangles and have the same area. The triangle is their common overlap, so the regions and have the same area. Therefore the pink region has area .