Notes
three regular hexagons solution
Three Regular Hexagons
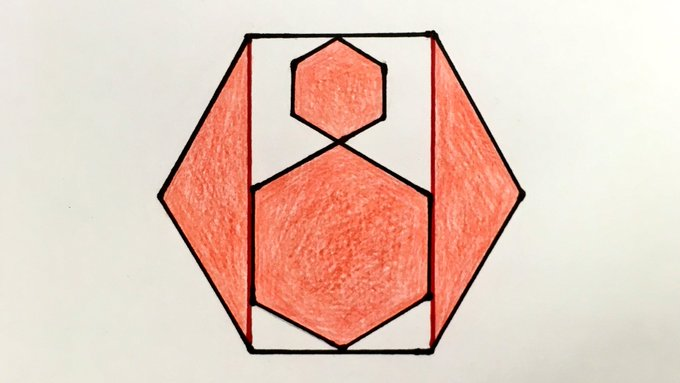
Three regular hexagons. What fraction is shaded?
Solution by Lengths in a Regular Hexagon
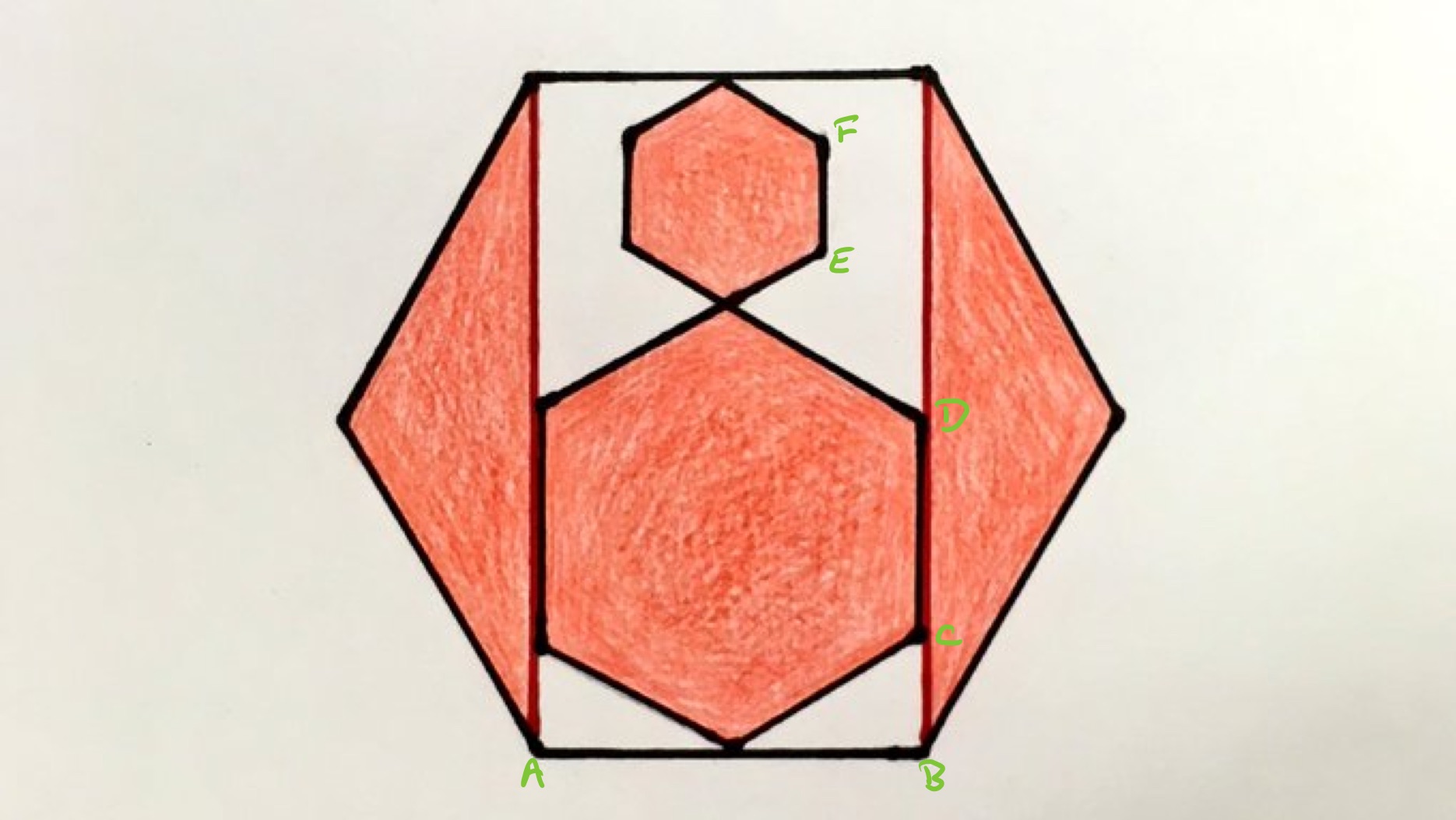
Let , , be the side lengths of the three hexagons in ascending order. Using the relationships between the lengths in a regular hexagon, the height of the middle hexagon is times its own side length and is also , so . The distance across a hexagon from vertex to vertex is twice the side length so the height of the largest hexagon is , so . This shows that , and so .
The area of the middle hexagon is therefore times that of the smallest, and the area of the largest hexagon is times that of the smallest. The two side triangles consist of one third of the area of the full hexagon, so are times the area of the smallest. Therefore the shaded area comprises times that of the smallest hexagon. The fraction that is shaded is then of the outer hexagon.